Wave pressure and velocity

Susan Hautala

52 Wave pressure and velocity

A nice visualization of the sea surface height and water parcel motions can be found on Dan Russell’s webpage Longitudinal and Transverse Waves (see the Water Waves animation), where you can see that it is a combination of these two types of motion. Here we will find expressions for the water parcel motion associated with a propagating sinusoidal wave in sea surface height, using fluid mechanics.

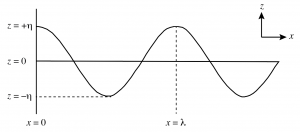
Snapshot in time of an ocean surface wave in the vertical plane.

We first define the vertical displacement, often written using the symbol $\eta$ , of water parcels with respect to their equilibrium position in the Earth’s gravity field. For water parcels at the sea surface this equilibrium position would be z = 0. Because this disturbance of the sea surface creates disturbances in the pressure field, it will result in accelerations of fluid parcels. For the purposes of developing understanding, we will make the assumption that pressure is hydrostatic. This is equivalent to assuming that horizontal pressure gradients do not change with depth, which will be true if the wavelength of the wave is long compared to the water depth. We start with a wave propagating toward the positive x direction,

$\eta = A \hspace{2pt} cos(kx-\omega t).$

Here, $A$ , the amplitude of the wave, is equal to half of the distance between the crest and the trough (that latter distance is also known as the wave height). The hydrostatic pressure gradient force related to this sea-surface displacement is

$PGF=-\frac{1}{\rho_0}\frac{\partial P}{\partial x}=-g \frac{\partial \eta}{\partial x} = Agk \hspace{2pt} sin(kx-\omega t).$

If no other forces are acting, then this pressure gradient force will create a cyclical acceleration and deceleration in the x direction as it changes sign,

$\frac{\partial u}{\partial t}=PGF=Agk \hspace{2pt} sin(kx-\omega t).$

We can integrate the acceleration with respect to time to determine the velocity field,

$u=\int Agk \hspace{2pt} sin(kx-\omega t) \hspace{2pt} dt = Ag\frac{k}{\omega} \hspace{2pt} cos(kx-\omega t).$

Note that the horizontal velocity has the same phase as the sea surface displacement – there is maximum motion of water parcels in the direction of propagation under the wave crests. For this hydrostatic case, the horizontal velocity is the same at all depths.

The amplitude of the wave for vertical velocity ranges from zero at the fixed sea floor to $w=\partial \eta / \partial t$ at the sea surface, so it is also a cyclical function. It has a 90° phase shift to sea-surface displacement, with positive values in front of the crest, and negative values behind, tracking the rising and then falling sea surface.

Key Takeaways

These are the sea-surface displacement and horizontal velocities for a hydrostatic ocean surface wave propagating in the x direction in water of (resting) depth h:

$\eta = A \hspace{2pt} cos(kx-\omega t)$