36 Ekman pumping
If there is convergence or divergence of Ekman transport, then there will be upwelling or downwelling at the base of the Ekman layer.
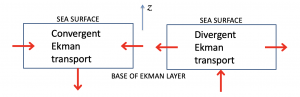
The vertical velocity at the base of the Ekman layer is often referred to as Ekman pumping. It can occur near boundaries, where an along-shore component of the wind stress creates a coastal divergence (or convergence) in the Ekman layer. It can occur at the equator, where the direction of the Ekman transport due to wind blowing along the equator changes sign. Finally, it can occur in the ocean interior because of gradients in wind stress.
We start by dividing the Ekman transport by the thickness of the Ekman layer (
) to find the vertically-averaged velocity. For example for the x-component of Ekman transport
![\[ \overline{u} = \frac{Transport_{Ekman}^x}{H}= \frac{1}{f \rho_0 H}\tau_{WIND}^y \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-22934cae1fa9f99aa5356c62674a2ee4_l3.png "Rendered by QuickLaTeX.com")
Next, form the horizontal divergence of the vertically-averaged velocity components in the x– and y– directions
![\[ \frac{\partial \overline{u}}{\partial x}+\frac{\partial \overline{v}}{\partial y} = \frac{1}{\rho_0 H}\left(\frac{\partial}{\partial x}\frac{\tau_{WIND}^y}{f}-\frac{\partial}{\partial y}\frac{\tau_{WIND}^x}{f} \left) = \frac{1}{\rho_0 H} \nabla \times \frac{\underline{\tau}}{f} \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-598dd00a784095790dc9a207d594842d_l3.png "Rendered by QuickLaTeX.com")
where we have used the definition of the curl operator. Now, equate the horizontal divergence to the vertical convergence
![\[ -\frac{\partial w}{\partial z} = -\frac{w(0)-w(-H)}{H}= \frac{w(-H)}{H}=\frac{\partial \overline{u}}{\partial x}+\frac{\partial \overline{v}}{\partial y}= \frac{1}{\rho_0 H} \nabla \times \frac{\underline{\tau}}{f} \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bcadc241b86c03210240f80b49e84caa_l3.png "Rendered by QuickLaTeX.com")
Since there is no vertical velocity at the sea surface, the left side becomes the vertical velocity at the base of the Ekman layer, 
, divided by the Ekman layer thickness, 
. Since 
appears on both sides of the equation, we can divide it out.
Key Takeaways
The vertical velocity at the base of the Ekman layer, also known as the Ekman pumping rate is
![\[ w_{Ekman}=\frac{1}{\rho_0}\nabla \times \frac{ \underline{\tau} }{f} \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1e0378f817bce4d454aa1e3f0127ee18_l3.png "Rendered by QuickLaTeX.com")
Note:
Sometimes you will see only downward (negative) velocity at the base of the Ekman layer referred to as Ekman pumping, with positive velocity referred to as Ekman suction.
Media Attributions
- EkmanPumpingSchematic © Susan Hautala is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
