"

33 Geostrophic balance

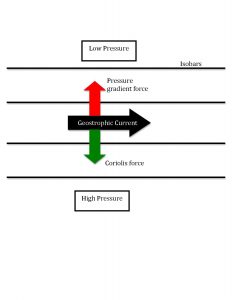
Sketch of an example force balance involved in geostrophic flow in the northern hemisphere. Pressure contours are straight lines aligned with the x-axis (eastward) in this example, with higher pressure in the south. The pressure gradient force points towards positive y (northward) and is balanced by the Coriolis force pointing to the south. This Coriolis force is associated with a geostrophic current vector that is directed to the east.
Schematic of geostrophic flow in a horizontal plane in the Northern Hemisphere. The Coriolis force is directed in the direction opposite to the Pressure Gradient Force, implying a current along constant pressure lines.

 

If the Rossby number is low, then rotation is important.  The steady-state force balance between the Coriolis force and the pressure gradient force is called geostrophic balance and is the approximate state of most large-scale flows in the ocean and atmosphere.  For example, the y-component momentum equation in geostrophic balance (see figure at left) would be written:

    \[ 0 = -fu-\frac{1}{\rho_0}\frac{\partial P}{\partial y} \]

Since the current vector is perpendicular to the Coriolis force, it is also perpendicular to the pressure gradient. Flow is thus along lines of constant pressure, called isobars, rather than down the pressure gradient as we would intuit from the smaller scales of our everyday experience.

Key Takeaways

If the pressure field is known, then the geostrophic velocity components can be directly calculated as:

    \[ u =- \frac{1}{f \rho_0 }\frac{\partial P}{\partial y} \]

    \[ v = \frac{1}{f \rho_0 }\frac{\partial P}{\partial x} \]

However, unlike the atmosphere, the pressure field in the ocean is quite difficult to measure. Near the surface of the ocean, the shallow pressure field can be measured by satellite altimeters. The shallow pressure is related hydrostatically, P=g \rho_0 \eta, to the elevation of the sea surface, \eta relative to its equilibrium geopotential, z = 0.

This technology alone is particularly useful for detecting how currents change in time because estimates of the time-mean state require knowledge of the gravity field with a high degree of accuracy.

Key Takeaways

The near-surface geostrophic flow can be calculated from sea surface height as:

    \[ u_{surface} =- \frac{g}{f }\frac{\partial \eta}{\partial y} \]

    \[ v_{surface} = \frac{g}{f}\frac{\partial \eta}{\partial x} \]

In the interior ocean, we cannot measure horizontal pressure gradients directly, but we can use CTD data to measure dynamic height, related to the difference in the pressure gradient between two levels in the vertical.

Key Takeaways

Differences in geostrophic velocity in the vertical (between two pressure levels) can be found from measured horizontal dynamic height gradients:

    \[ u(P)-u(P_{REF}) =- \frac{1}{f }\frac{\partial D}{\partial y} \]

    \[ v(P)-v(P_{REF}) = \frac{1}{f}\frac{\partial D}{\partial x} \]

where in this case

    \[ D=-\int_{P_{REF}}^{P}\frac{1}{\rho}dP \]

A common assumption about the reference level (P_{REF}) velocity is that it is zero at some deep level (i.e., that it is much smaller than the velocity of interest, typically a stronger, shallower flow).  Alternately, the geostrophic velocity can be measured directly at the reference level.

 

Satellite image of sea surface height (dynamic height) in the Gulf of Mexico with a color scale ranging from 40 to 250 dynamic centimeters. Geostrophic current vectors are superimposed showing clockwise flow around centers of high dynamic being.
The map shows the geostrophic currents field in the Gulf of Mexico. The background image represents the dynamic height.

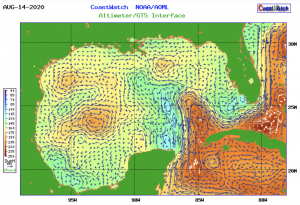
This map shows geostrophic currents on a particular day. First, an estimate of the time-mean geostrophic circulation is made that applies near the surface of the ocean, using an optimal fit to combined data from satellite altimeters, density profiles, and drifting buoys.  This time-mean field is then added to the time-variable field (that can accurately be determined from altimeter data) to produce daily operational maps of ocean currents.

Mini-lectures for class:

 

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book