35 The Ekman layer

If friction is important, as in the boundary layers near the ocean surface and sea floor, then an ageostrophic component of the flow will be present. Ageostrophic refers to that part of the total velocity vector that is not in geostrophic balance with the pressure gradient force. In time-dependent problems, it may refer to a component of flow accelerating down the pressure gradient. In a steady-state situation, it may refer to a component of the flow resulting from balance between the Coriolis force and the shear stress.

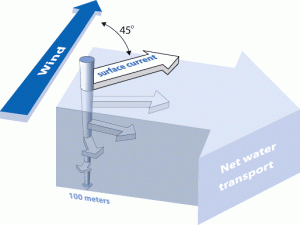
The Ekman spiral occurs as a consequence of the Coriolis effect. When surface water molecules are moved by the wind, they drag deeper layers of water molecules below them. Like surface water, the deeper water is deflected by the Coriolis effect—to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. As a result, each successively deeper layer of water moves more slowly to the right or left, creating a spiral effect.

A momentum balance between Coriolis and frictional stress is called the Ekman balance, and it is typically sizeable in the frictional boundary layer near the top and bottom of the ocean, called the Ekman layer. Steady-state ageostrophic currents in the Ekman layer take the form of a spiral that decays with depth and a sense of rotation that is of opposite sign in the Northern and Southern Hemispheres. In large-scale oceanography, we are usually not concerned with the details of the currents in the Ekman layer, but with the net transport. The Ekman transport is directed perpendicular to the direction of the wind stress, to the right of the direction of the wind in the Northern Hemisphere.  

For example, for the x-component of wind-stress (resulting in a y-component of transport), we start with the steady-state balance between Coriolis and the net force (per unit mass) due to frictional stress:

    \[ 0 = fv+\frac{1}{\rho_0}\frac{\partial \tau^x}{\partial z} \]

    \[ v = -\frac{1}{f \rho_0}\frac{\partial \tau^x}{\partial z} \]

Then integrate vertically from the base of the Ekman layer (defined to be the level where the frictional stress vanishes) to the sea surface:

    \[ Transport_{Ekman}^y=\int_{-H}^0 v dz = -\frac{1}{f \rho_0}\int_{-H}^0\frac{\partial \tau^x}{\partial z} = -\frac{1}{f \rho_0}\left(\tau_{WIND}^x-0 \right).\]

where we have used the fact that the stress at the sea surface is equal to the wind-stress and that the stress is zero, by definition, at the base of the Ekman layer, z=-H.

Key Takeaways

The final expressions for Ekman transport are

    \[ Transport_{Ekman}^x= \frac{1}{f \rho_0}\tau_{WIND}^y \]

    \[ Transport_{Ekman}^y= -\frac{1}{f \rho_0}\tau_{WIND}^x \]

Note that the units here are m^2/s. This is because it is transport per unit distance perpendicular to the transport.

Want more explanation? The following video gives a nice qualitative overview of the Ekman layer, transport and consequences for upwelling and downwelling that we will consider in the next section.

 

 

 

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book