Deep- and shallow-water waves

Susan Hautala

51 Deep- and shallow-water waves

Ocean surface waves have a dispersion relationship with a wave speed that is, in general, dependent on wavelength,

$C_{Phase}^2 =\frac{\omega^2}{k^2}= \frac{g}{k} \hspace{2pt} tanh(kh).$

such that these waves are in general dispersive. (You are not responsible for the derivation of this expression, just for understanding its implications.) This dispersive behavior, where longer wavelength waves travel faster than shorter wavelength waves, is familiar if you have observed ripples spreading outward from a stone cast into a pond (watch the following YouTube video if you can’t remember what that looks like!) These ripples occur in water that is deep relative to their wavelength.

However, when the water is shallow relative to the wavelength of the wave, the waves become nondispersive. Tsunamis are an example of such long wavelength waves, but even waves created by storms can become nondispersive when they approach the shoreline and enter shallow water.

We start to understand this different behavior in deep vs. shallow water by taking a look at the hyperbolic tangent function

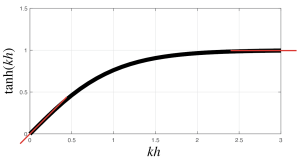
Plot of the hyperbolic tangent of the product of wavenumber and depth. Also shown in red are tangent lines with slopes of 1 (left) and 0 (right).

For small kh, which will occur for long wavelength waves (relative to water depth), the function can be approximated by a line with slope = 1. In this case, where $tanh(kh) \approx kh$ the phase speed is approximately

$C_{Phase}^2 = \frac{g}{k} \hspace{2pt} kh = gh \quad\quad C_{Phase}=\sqrt{gh}.$

The dispersion relationship is $\omega = \sqrt{gh} k$ , which has first derivative, $\partial \omega / \partial k$ that is equal to the phase speed,

$C_{Group}=C_{Phase}= \sqrt{gh}$

These waves are called shallow water waves.

For large kH, which will occur for short wavelength waves, the function can be approximated by a line with slope = 0. In this case, where $tanh \approx 1$ , the phase speed is approximately