"

59 Scattering

Like other waves, electromagnetic energy refracts and diffracts. And while the speed of light in a vacuum is constant, the speed of light through materials varies, and can be a function of wavelength, leading to such phenomena as the separation of colors (i.e., different wavelengths of light) when light passes through a prism. This is a form of dispersion.

A general wave phenomenon that we have not considered before is scattering.  Scattering is a term used to describe the interaction of waves with bodies of similar, or smaller, size to the wavelength. (When waves encounter bodies that are large relative to wavelength, they reflect.) These interactions can lead to wave energy redirected over the full 360° relative to the angle of incidence.

Diagram of the Rayleigh scattering function. The top panel shows vectors spreading from a central scattering point, showing symmetrical larger vectors in both the direction of propagation ("incident") and the opposite direction ("reflected" or "backscattered"). The scattering angle is defined in a diagram to indicate the direction counter-clockwise from the incident direction. The bottom panel shows intensity (vector length) as a function of scattering angle from zero to 360°, with maxima at 0° and 180°.
Representations of the theoretical Rayleigh scattering function. Top: arrows indicate directions of scattered energy relative to incident energy directed to the right, with length indicating the relative intensity in each direction. Bottom: relative scattered intensity (y-axis) as a function of scattering angle (x-axis). 0° corresponds to the angle of incidence.

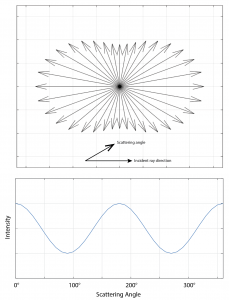
Theoretical scattering functions predict the energy as a function of scattering angle relative to the angle of incidence, but the distribution can also be measured empirically. One common theoretical function is Rayleigh scattering (shown in the figure), which is applicable to encounters with particles with diameters that are small compared to the wavelength.

The amount of energy scattered under this theory is inversely proportional to wavelength, and increased scattering of blue light by atmospheric gas particles is thought to be responsible for the color of the sky, as discussed on the Hyperphysics webpage about scattering and a blue sky.

For larger particles, relative to wavelength, the distribution of relative intensity with respect to scattering angle becomes asymmetric, with more energy scattered into the forward direction (i.e., at small scattering angles). This class of scattering is referred to as Mie scattering. Mie scattering is not strongly wavelength dependent.

Mini-lecture for class:

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book