Bulk Impedance

Susan Hautala

48 Bulk Impedance

When fluid motion is “channelized”, i.e., water parcels are moving back and forth between boundaries in a uniform way, then the geometry of the channel can create a kind of impedance, even in the absence of any changes in fluid properties. We define a bulk impedance that defines the ratio of pressure to fluid transport oscillations (rather than water parcel velocity oscillations as for the fluid impedance). Bulk impedance is an important consideration for the acoustics of pipes and horns, as well as the shallow water limit of ocean surface waves (that we will consider in more detail next week).

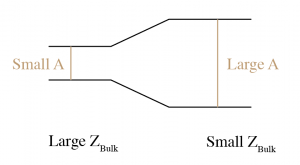
Schematic for a flared wind instrument in relation to its bulk impedance.

For example, consider a horn that is flared toward one end. The fluid or specific impedance, $Z=\rho C$ , is constant within the pipe. However, the velocity of air parcels in the sound wave created by applying a given pressure to the small end of the horn decreases along the pipe, because fluid continuity requires that the transport through any cross-section be a constant, $uA=const.$ Thus the same amount of pressure creates smaller fluid velocity oscillations in the flared end, with larger cross-sectional area, than in the small end. To account for this behavior, we define the bulk impedance associated with the instrument as

$Z_{Bulk}=\frac{Pressure}{Transport}=\frac{P}{uA}=\frac{Z}{A}.$

In terms of shallow water ocean surface waves, a similar phenomenon occurs, regulated by the depth of the ocean.

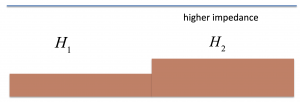
Schematic for variations in bulk impedance for shallow-water ocean waves, in connection to a depth change. The water layer is between the top of the brown color (seafloor) and the solid line.

For this limit of ocean surface waves, water parcel velocity oscillations are the same at all depths, extending from the top of the ocean to the seafloor. Consider two waves with the same wave pressure amplitude (related to the sea surface displacement), but one is propagating in shallower water than the other. In the shallower domain the depth is a constant $h=H_2$ , and in the deeper domain $h=H_1$ . The same amplitude sea-surface disturbance will create the same amplitude water parcel motion, $u,$ but will be associated with a smaller transport oscillation in shallower water, $uH_2 < uH_1.$ We can define a bulk impedance,