1 Coordinates

To mathematically describe variables in the ocean, we need three dimensions of space and one dimension in time.  With more than one spatial dimension, position becomes a vector of distances along each dimension from some origin (0,0,0).

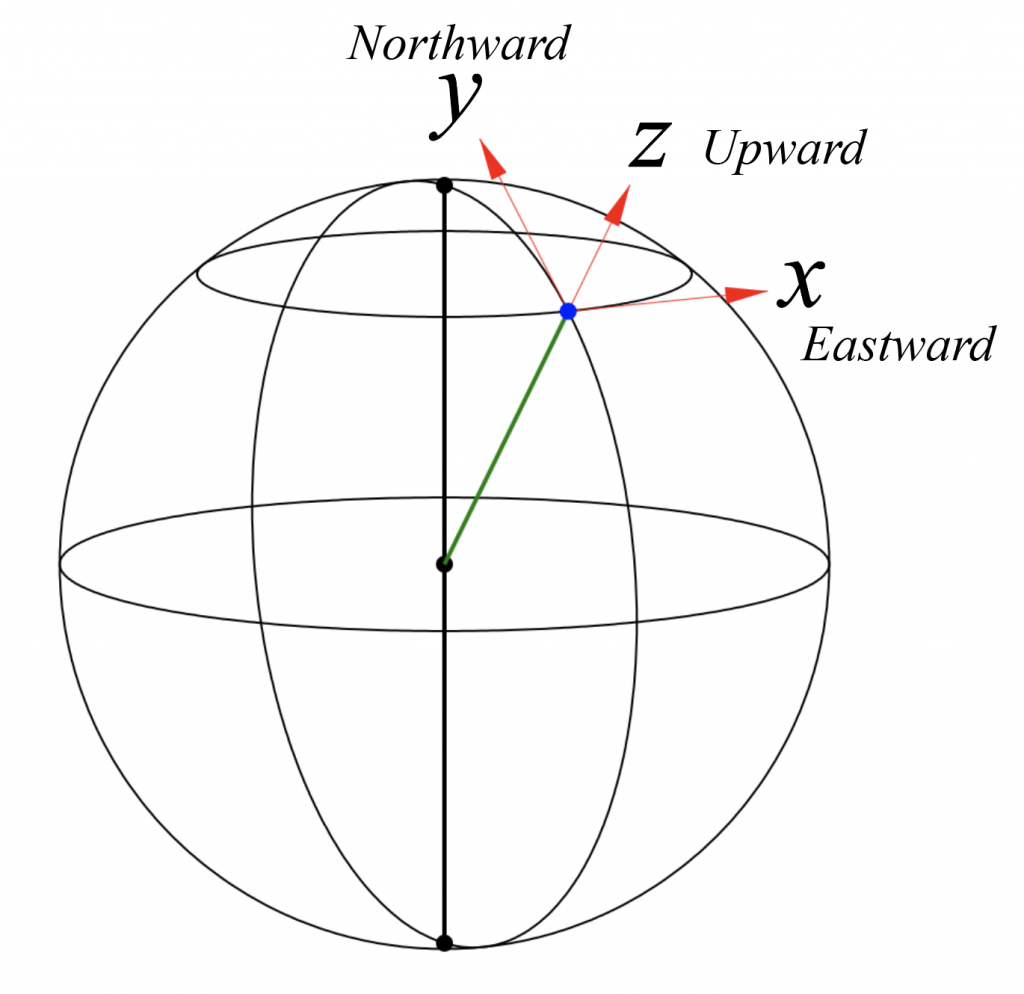
Often (and almost always in this class) it is convenient to use a local Cartesian coordinate system for a plane tangent to the Earth’s surface.  We write:

    \[ \underline{\textbf{x}}=(x, y, z) \]

The Standard Open-Ocean Coordinate System

x increases to the East along the local horizontal plane, in the direction of increasing longitude

y increases to the North along the local horizontal plane, in the direction of increasing latitude

z increases upward in the local vertical direction

z = 0 is at the surface of the ocean (to be precise: where the ocean surface would be if there were no motion, i.e., the surface of a resting ocean in equilibrium with Earth’s gravity aka geopotential field).

Cartesian coordinates on a sphere
The local Cartesian coordinates for a point on the surface of the Earth at the blue dot.

Unit vectors have length = 1.  You can create a unit vector in any direction by dividing the vector by its magnitude.  In physics, this means that you have divided out the units and so the vector is dimensionless.

Special symbols are often given to unit vectors in the directions of the coordinate system axes.  In our (x,y,z) = (Eastward, Northward, Upward) coordinate system:

    \[ \hat{i}=(1,0,0) \]

    \[ \hat{j}=(0,1,0) \]

    \[ \hat{k}=(0,0,1) \]

A few details are important about this coordinate system:

  • z will be generally be negative within the ocean and positive within the atmosphere.  Depth is a positive number that represents the distance below the ocean surface. Larger negative numbers are found deeper in the ocean. We can write the z value for a water parcel found at a depth of h meters below the (resting) ocean surface as z=-h.
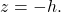
  • The absolute orientation of this standard local Cartesian coordinate system changes depending on where you are on the Earth (i.e., the direction of “Up” differs if seen from outer space).
  • The system isn’t universal in oceanography, but is widely used in studying large-scale systems.  Coastal or estuarine problems often use a different local Cartesian coordinate system that matches the important geography of the system.  For example, x might point along the coastline, with y pointing offshore.
  • The rate of moving through space in each direction, the velocity, will also be a three-dimensional vector, \underline{\textbf{u}}=(u, v, w).

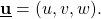
FYI:  Latitude and longitude come from a spherical coordinate system. Longitude is the angle counterclockwise looking down on the north pole relative to 0° passing through Greenwich, England.  Latitude is the angle counterclockwise looking down at the Earth from above the equator (0° corresponds to the eastward direction along the equator). Elevation (formally: distance from the center of the Earth) is the third coordinate in this system.

Converting Latitude and Longitude (in Degrees) to Distance Units

  • On the surface of the Earth, there are 111 km distance in every degree of latitude.
  • The distance between longitude lines decreases towards the poles.  You can calculate the distance between 1 degree of longitude as 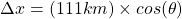\Delta x=(111 km)\times cos(\theta), where 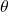\theta is the latitude.

 

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book