27 The shear stress
In the previous chapter, we considered two plates bounding a region of fluid with flow parallel to the plates. We define the stress to be the horizontal contact force per unit area, where the magnitude of the force is the amount that must be applied to keep this system in motion in the presence of friction. Since, by Fick’s Law, the magnitude of the stress is proportional to the velocity gradient in the perpendicular direction, i.e., the shear, we call this form of frictional stress the shear stress. By convention, the sign of the shear stress is chosen to match the sign of the shear. This means that its sign is opposite to the sign of the momentum diffusion (the latter is directed down the gradient, and thus has the opposite sign to the shear).
Key Takeaways
The “diffusive momentum flux” can be represented as a force per unit area of a surface called the viscous stress or shear stress.
![\[ \tau^x=\rho \nu \frac{\partial u}{\partial z} = - \rho \times Diffusive Flux \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fe0b9ff33f64f1c61f88347c4667e1bb_l3.png "Rendered by QuickLaTeX.com")
where the Greek symbol 
(“nu”) is the molecular viscosity (aka diffusivity) for momentum. In a turbulent fluid, this is typically replaced with a larger turbulent diffusivity, as discussed below.
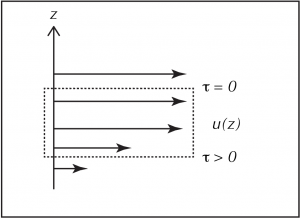
Now consider a water parcel surrounded by other water parcels above and below where the shear may be different at the top and at the bottom. In the example sketched above, the force on the lower interface acting toward negative x is greater than the force on the upper interface acting toward positive x and the fluid will decelerate.
The net force is given by the difference in force acting at the top and bottom surfaces of the control volume, i.e., the gradient in shear stress.
![\[ \frac{Du}{Dt}=\frac{Force^{TOP}-Force^{BOTTOM}}{Mass}=\frac{\left(\tau^{TOP}-\tau^{BOTTOM}\right)\Delta x \Delta y}{\rho \Delta x \Delta y \Delta z}=\frac{1}{\rho}\frac{\partial \tau}{\partial z} \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3cf70df15541f9ba3a19033e06c60e1b_l3.png "Rendered by QuickLaTeX.com")
Key Takeaways
Since shear stress is proportional to the velocity gradient, we can write the Lagrangian acceleration caused by the net frictional force using either 
or u.
![\[ \frac{Du}{Dt}=\frac{1}{\rho}\frac{\partial \tau^x}{\partial z}=\nu \frac{\partial^2 u}{\partial z^2} \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7e6c37fd73e6860213f285577b24fe84_l3.png "Rendered by QuickLaTeX.com")
The latter representation is directly analogous to the diffusion term in our tracer equations. It is equal to minus one times the diffusive flux divergence. In the example above, the second derivative of the velocity is negative (the positive velocity gradient decreases to zero moving upward). Less momentum is diffusing into the control volume from above than diffusing out from below.
As for water properties, when modeling large scale oceanographic flows, the molecular viscosity is often replaced by a much larger turbulent momentum diffusivity (derivation), usually written K or A, related to the turbulent flux of momentum (
), such that
![\[ \frac{Du}{Dt}=-\frac{\partial \left(\overline{u'w'}\right)}{\partial z}=\frac{1}{\rho}\frac{\partial \tau^x}{\partial z}=K \frac{\partial^2 u}{\partial z^2}\]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7bd9694b726b0dc5be8073e86c021e14_l3.png "Rendered by QuickLaTeX.com")
Media Attributions
- Nonuniform_shear © Susan Hautala is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
