5 Partial Derivatives
For a function of one independent variable, say x, the derivative gives information about how the function, say ![]() , changes when x changes. This is the meaning of the first derivative.
, changes when x changes. This is the meaning of the first derivative.
![]()
In other words, if you make a small but finite change ![]() , you get a change in the value of the function
, you get a change in the value of the function ![]() . The derivative is the ratio of these two changes, taken in the limit when
. The derivative is the ratio of these two changes, taken in the limit when ![]() becomes very small. A geometrical interpretation is that the derivative is the slope of a tangent line. The derivative can also be a function of x (i.e., in the picture below, the slope of the tangent line will change as you move in x).
becomes very small. A geometrical interpretation is that the derivative is the slope of a tangent line. The derivative can also be a function of x (i.e., in the picture below, the slope of the tangent line will change as you move in x).
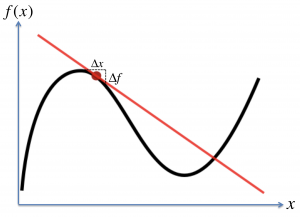
When we have something that is a function of multiple independent variables (like x, y, z and t), we define an equivalent operation that tells us how the function changes when just one of the independent variables changes and all the others are kept constant. This is called the partial derivative. It is written with a special symbol “![]() ” instead of the “d”.
” instead of the “d”.
![]()
and has the meaning of a change in f divided by a change in x calculated while holding all the other independent variables constant.
Key Takeaways
In fluid mechanics, we often write the operation of taking the derivative in each of the spatial dimensions as a vector operator:
![]()
While this may seem a bit abstract, the next two sections will be about two applications of this vector operator, in order to calculate the gradient and the divergence. These quantities will be fundamental to what we do in the rest of the course.
We’ve already implicitly used partial derivatives when we discussed a three-component velocity vector. Recall from physics that the velocity in one direction is the change in distance divided by the change in time. Taken to infinitesimal changes, this becomes the first derivative of space (x) with respect to time (t).
![]()
Velocity in three dimensions is written with partial derivatives in each direction:
![]()
For example, the first component of the velocity vector, u, is the rate at which a water parcel increases distance in the eastward direction (x). If the first component is positive
![]()
then the water parcel has a component of motion towards the east. If this partial derivative is negative, then it has a component of motion toward the west.
Media Attributions
- DerivativeTangent © jacj adapted by Susan Hautala is licensed under a CC BY-SA (Attribution ShareAlike) license

