8 The Divergence

The divergence of a vector is the sum of the partial derivatives of its components with respect to their individual coordinates.

Key Takeaways

The divergence of a vector \underline{\bold{F}}, written in terms of its components in our usual coordinate directions \underline{\bold{F}}=(F^x,F^y,F^z)  is defined as:

    \[ \nabla \cdot \underline{\bold{F}}=\frac{\partial F^x}{\partial x}+\frac{\partial F^y}{\partial y}+\frac{\partial F^z}{\partial z} \]

You can get an intuitive feel for the divergence by sketching vectors in space and thinking about how these vectors are tending to stretch out or squash the distance between.

Examples

Here are some examples of vector fields, and the sign of their divergence in a horizontal plane:

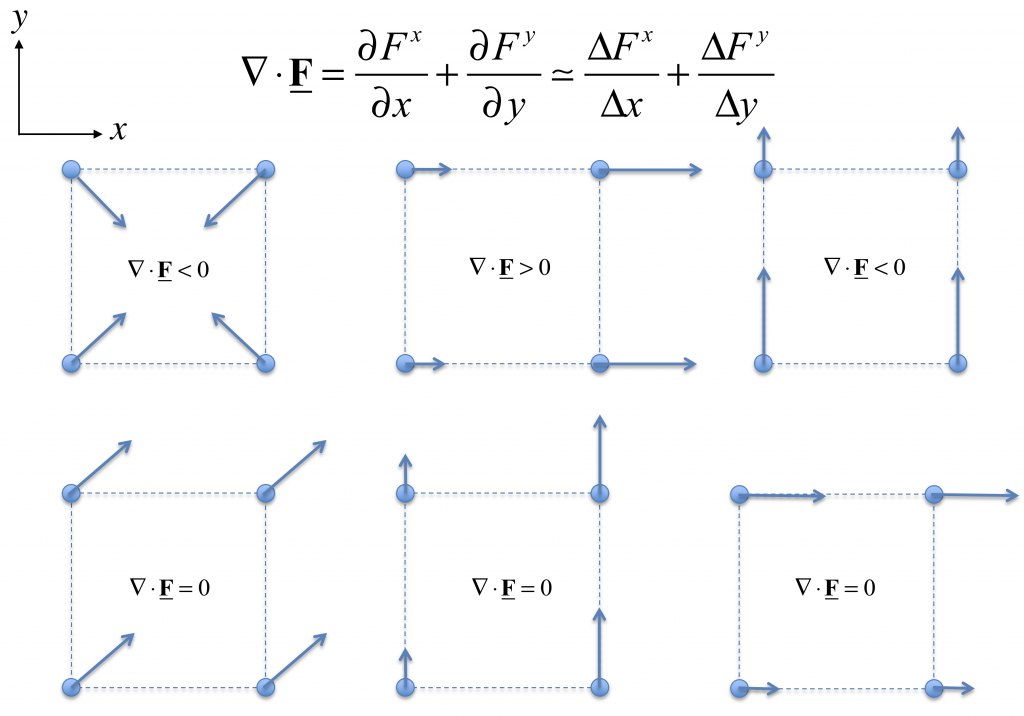
We will be considering the divergence of vector fields that represent the flux of some property like salinity, or oxygen, or momentum, in the ocean. Here, an important special case occurs when we consider the flux of water itself. In this case the flux vector is just the velocity vector, \underline{\bold{u}}=(u,v,w), and the divergence is zero, \nabla \cdot \underline{\bold{u}}=0. We will discuss this in more detail later.

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book