12 Flux Divergence and Conservation

While there cannot be a net transport of water across the sides of a control volume in the ocean, there can be a net transport of substances dissolved in the water. For example, phytoplankton could produce oxygen inside the box, leading to greater flux of oxygen leaving the control volume than entering it.

Any net transport out of the box must be associated with a divergence of the flux inside the control volume (via the divergence theorem).  But any net transport into or out of the volume will also be associated with a raising or lowering of the concentration of stuff inside (if there are no other processes to compensate the divergence).  We can mathematically equate these two consequences of net transport to create conservation equations for scalar properties in the ocean.

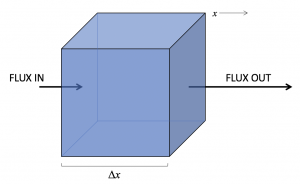
Sketch of a positive flux divergence contribution from changes in the x-direction, associated with more transport leaving the control volume than transport entering.

In the sketch above, more of a substance is leaving than entering the control volume which (in the absence of a source inside) will lead to a decrease over time of its concentration.  This is also the situation of a positive divergence of the vector flux field.  We can show (see derivation) that the contribution from this divergence in the x-direction is:

    \[ \frac{\partial C}{\partial t}=-\frac{\partial F^x}{\partial x}, \]

where C is the concentration of the substance inside the box, and F^x is the x-component of its flux vector.

We can add variations in the other dimensions to get a general expression for how the divergence of a flux relates to a change in concentration over time:

Key Takeaways

A positive flux divergence leads to a decrease in concentration over time (in the absence of any compensating other processes):

    \[ \frac{\partial C}{\partial t}=-\frac{\partial F^x}{\partial x}-\frac{\partial F^y}{\partial y}-\frac{\partial F^z}{\partial z}=-\nabla \cdot \underline{\textbf{F}} \]

For the advective flux, recall that \underline{\textbf{F}}=\underline{\textbf{u}}C.  We can show (see derivation) that the divergence of the advective flux is:

    \[ \nabla \cdot \left( \underline{\textbf{u}}C \right) =\underline{\textbf{u}} \cdot \nabla C \]

Key Takeaways

The advective contribution to changing concentration over time is

    \[ \frac{\partial C}{\partial t}\biggr|_{ADV}=-\underline{\textbf{u}} \cdot \nabla C=-\left(u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}+w\frac{\partial C}{\partial z}\right).\]

The right side is minus 1 times the advective flux divergence.  If the divergence is positive, the concentration in the control volume will decrease over time (the left side).

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book