56 The decibel scale

A good overview of the decibel scale, a logarithmic scale very commonly used in acoustics, can be found on DOSITS webpage Introduction to Decibels. It might be helpful to review the logarithm laws.

Common sounds and their decibel sound levels relative to the different air and water reference values.

Sound is typically measured in the ocean with instruments, hydrophones, that record pressure (P) variations, and the intensity, I=P^2/(\rho C), can be calculated from the sound pressure along with properties of seawater. (For an overview of how sound speed in seawater varies with temperature, salinity and pressure, see the DOSITS webpage Tutorial: Speed of Sound.)

Key Takeaways

The sound level in decibels (dB) is calculated from a measured intensity (I) or sound pressure (P) amplitude as

    \[dB = 10 \hspace{2pt} log_{10} \left( \frac{I}{I_0} \right)=20 \hspace{2pt} log_{10} \left( \frac{P}{P_0} \right) \]

where I_0 = 6.7 \times 10^{-19} W m^{-2} and P_0=1 \mu Pa correspond to standard marine reference values, assumed to be measured at 1 meter from the sound source.
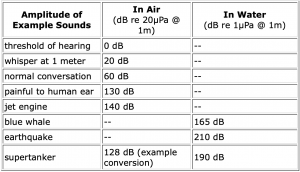
Note: Be careful – marine reference values are not the same as in air!

Here we will look at formulas for spherical and cylindrical spreading in the decibel scale. When using decibels, the term transmission loss, is often used to describe the number of decibels of sound level that are lost over a given distance. The decibel scale is particularly convenient because transmission loss terms along different segments of a total ray path can be added to determine the total loss of signal strength. Transmission loss is a positive number although it represents a loss term for acoustic energy.

For spherical spreading, we found that I/I_0=1/r^2. In terms of decibel transmission loss (TL), this becomes

    \[ TL=-10 \hspace{2pt} log_{10} \left( \frac{I}{I_0} \right)=-10 \hspace{2pt} log_{10} \left( r^{-2} \right)=20 \hspace{2pt} log_{10}(r), \]

where it is assumed that r is given in meters (because the reference distance is in meters).

Similarly, for cylindrical spreading,

    \[ TL = -10 \hspace{2pt} log_{10} \left( r^{-1} \right)=10 \hspace{2pt} log_{10}(r). \]

Key Takeaways

Transmission losses (TL) for spherical and cylindrical spreading can be calculated in decibels as

    \[ TL_{spherical} = 20 \hspace{2pt} log_{10}(r) \]

    \[ TL_{cylindrical} = 10 \hspace{2pt} log_{10}(r) \]

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book