53 Wave rays and energy conservation

Shallow water waves have a phase speed that is dependent on water depth, as considered in the last section. Thus, the ocean presents a medium for propagation where complex variations of wave speed can refract these waves, concentrating wave energy in some places, and diluting it in others. This phenomenon impacts societally important problems such as predicting tsunami intensity and understanding shoreline erosion under the action of incoming waves from the open ocean.

Let’s start with wave energy. You are not responsible for the derivation in this class, but the total (kinetic + potential) wave energy (per unit area of the sea surface) is

The wave energy flux is E multiplied by the wave’s propagation velocity. In general, we would want to multiply by the group velocity (as discussed, that is the rate at which wave energy moves through space), but for shallow water waves .

The units of wave energy flux are J m^-1 s^-1, representing the energy crossing a section of a vertically oriented plane that is 1 m along the wave crest times the full water column depth.

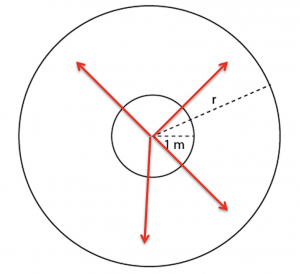
We define a wave ray as a line that is tangent to the wave velocity vector at every point in space, and we use wave rays to define pathways for the flow of energy. For shallow water waves, rays are perpendicular to the crests and tangent to the wavenumber vector. For example, for a point source (shown in the figure to the left), wave crests are concentric circles. Wave rays are radial lines directed outward from the source.

The wave energy flux per unit distance of crest will decrease moving outward from the source as the same amount of energy gets distributed over a larger and larger circumference (). For a constant depth ocean

For the more general case, as wave speed changes according to the bottom topography, there may be complicated geometries of wave rays leading to areas of more diffuse and more concentrated wave energy.

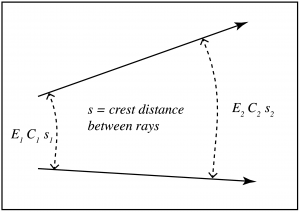
Since energy does not flow across wave rays, two wave rays define the sidewalls of a control volume for thinking about energy conservation.  Two crests define the other sidewalls. We define a variable s, that indicates the distance along wave crests between two wave rays, and imagine gradual changes along the pathway for both this distance and wave velocity.

Between points 1 and 2 in the diagram, the product of energy, wave speed and distance between rays must be a constant in order to conserve energy,

We can define such small control volumes to cover a domain of any size. Since the wave speed is known from bathymetry, it is possible to predict (for this friction-free system) the energy at any point in the ocean for a given wave source.