58 The electromagnetic wave spectrum

Each photon (i.e., quantum particle of electromagnetic energy) has a specific frequency () and wavenumber (k). We will use , “nu”, instead of for frequency here, as that is the most commonly used symbol in the field of electromagnetism. is a linear frequency reported in Hz (cycles per second).

Electromagnetic energy travels at a phase speed given by the ratio of frequency (converted to radians per second) and wavenumber . This speed of light in a vacuum is one of the fundamental constants of the universe, and so we will write it with the subscript “0” to indicate that it is a constant.

Photon energy is linearly related to its frequency (inversely related to its wavelength), with the constant of proportionality, h, called Planck’s constant.

Like other waves, we can define the intensity (i.e., the energy flux) across each unit of area of a given surface (such as the ocean surface) as

At the quantum level, we understand that this field is not truly continuous, with , also known as the power, equivalent to the number of photons arriving at the surface per unit time. Both and are commonly used in oceanography to represent the energy flux of electromagnetic waves. is typically used in studies of the upper ocean light field, and is typically used when considering the planetary energy balance.

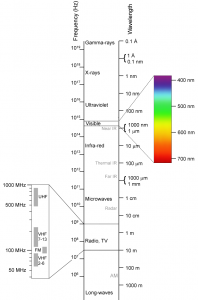
Electromagnetic energy occurs over a very wide range of wavelengths, and different names are given to different parts of the electromagnetic spectrum. In this class, we focus on two wavelength bands: the visible (about 380 to 740 nanometers, nm), and the infrared (740 nm to 1 mm).