25 The Bernoulli equation
We will now return to considering the energetics of fluid motion. You know from your first quarter physics class that any net force acting on a body will accelerate it, and thus change its kinetic energy. Let’s think about fluid flow energetics by looking at just at the x-component of the Navier-Stokes vector equation, i.e., the equation for the eastward component of motion (u):
![\[ \frac{Du}{Dt}=\sum F^x \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-81de23734ae5e94a0b8d29afd1efe978_l3.png "Rendered by QuickLaTeX.com")
This equation states that there will be Lagrangian acceleration of water parcels in the x-direction related to the net force in the x-direction, and is the fluid equivalent of Newton’s second law, 
. For now, we will consider only the pressure gradient force (PGF).
For frictionless flow, we can derive a relationship called Bernoulli’s Equation. We will start by stating it, and then use the momentum equation to better understand what it means.
Key Takeaways
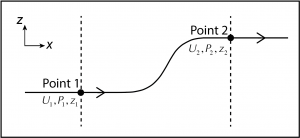
The Bernoulli Equation for two points (subscripts 1 and 2) along a streamline in frictionless, steady-state, incompressible flow is
![\[\frac{1}{2}{U_1}^2+\frac{P_1}{\rho_0}+gz_1=\frac{1}{2}{U_2}^2+\frac{P_2}{\rho_0}+gz_2\]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ee0c4b63c76d44127904e925bbd63578_l3.png "Rendered by QuickLaTeX.com")
Here, P is the pressure, U is the fluid speed, and z is the vertical elevation.
For our simplified situation where there is only flow in the x-direction (so that U=u), the Lagrangian acceleration (with no time-dependence) becomes
![\[ u\frac{\partial u}{\partial x}=PGF^x=-\frac{1}{\rho_0}\frac{\partial P}{\partial x}, \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-c6a9f062dd60e76941a1bc0032b422e6_l3.png "Rendered by QuickLaTeX.com")
where 
is the Pressure Gradient Force in the x-direction. Although the flow is steady at every point in space, there are spatial changes in velocity (accelerations following a water parcel that moves through space) – i.e. Lagrangian accelerations. We are now going to change the left side via a reverse chain-rule for differentiation:
![\[ \frac{\partial }{\partial x}\left(\frac{1}{2}u^2 \right)\approx\frac{\Delta KE}{\Delta x}=PGF \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8bd8ab194ea0458c42f0c0e79a99825e_l3.png "Rendered by QuickLaTeX.com")
In this form, we can see that the left side is telling us about the spatial gradient of kinetic energy (
). If the flow is overall eastward (at point 1, say), the PGF is causing an increase (if positive) or decrease (if negative) in the kinetic energy to the east along a streamline. (Note that as with many other quantities in a fluid, KE is per unit mass.) For two points separated by a distance 
, their difference in kinetic energy 
can be written as:
![\[ \Delta KE = \Delta \left(\frac{1}{2}u^2 \right)= PGF*\Delta x \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-816256692fab1ed260c6b086b193ad4f_l3.png "Rendered by QuickLaTeX.com")
The right side is the force times the distance, or the net work done on the system by the PGF which is needed to change the kinetic energy. Now we will substitute in our definition of the PGF:
![\[ \Delta KE =PGF*\Delta x \ =-\frac{1}{\rho_0}\frac{\partial P}{\partial x}*\Delta x=-\frac{1}{\rho_0}\Delta P \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-16d2b4535b9950c18074e4924a04972d_l3.png "Rendered by QuickLaTeX.com")
and if we write differences using values at point 2 minus point 1:
![\[\frac{1}{2}{u_2}^2 -\frac{1}{2}{u_1}^2=-\frac{1}{\rho_0}(P_2-P_1) \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d8d0fff38fb05d593513a27d602510df_l3.png "Rendered by QuickLaTeX.com")
or
![\[\frac{1}{2}{u_1}^2+\frac{P_1}{\rho_0}=\frac{1}{2}{u_2}^2+\frac{P_2}{\rho_0} \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5786009db539ee33d408fb95b57684db_l3.png "Rendered by QuickLaTeX.com")
which is starting to look like part of the equation in the box. Bernoulli’s Equation is really a statement of conservation of energy in the absence of friction.
Of course, it is not actually possible to have a change of just one component of velocity in space because of the continuity equation, so this simple example has to be modified to include at least one more component of velocity, with the kinetic energy in the shaded box at the top understood to represent the total kinetic energy.
If the vertical displacement is significant, then we also have to take into account changes in (geo)potential energy (PE = gz). The equation in the box is a general form of the Bernoulli Equation (we will not derive it) that is equivalent to:
![\[\Delta KE+\Delta PE=PGF*\Delta x \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fbf497c6b827f6e6fa48731cc2665e5c_l3.png "Rendered by QuickLaTeX.com")
where the KE is now related to the total flow speed, (
). In words, we could write this equation as “The sum of changes in kinetic plus potential energy (per unit mass) is equal to the work done by the pressure gradient force.” If you want more in the way of explanation and derivation of the term involving potential energy, see this Khan Academy lesson “What is Bernoulli’s Equation?”
Media Attributions
- BernoulliFigure © Susan Hautala
