44 Refraction

You can read about how refraction affects sound waves in Dan Russell’s online tutorial. Refraction, quantified by Snell’s Law, is a consequence of the fact that as waves move through space their frequency remains constant. If a wave passes through a change in phase speed in the medium, its wavelength must change in order for frequency to remain constant. Let’s work with a concrete example. For the “shallow water” limit of ocean surface gravity waves (as we will derive in a later section) the phase speed is related to water depth, h, by

    \[ C = \omega /\vert\underline{\textbf{K}} \vert = \sqrt{gh}. \]

When a wave approaches a change water depth (that impacts phase speed), then the direction of propagation will change according to Snell’s Law.  We can understand this by considering how individual components of the vector phase speed change at the depth transition boundary.

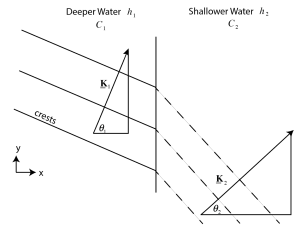
Schematic of wave refraction for a shallow water ocean surface wave crossing at an angle over a sharp depth change, associated with a reduction in wave phase speed.

In the sketch above there is a wave on the left approaching a sharp transition to shallower water.  Its crests are drawn as solid lines.  We define the normal line as a line that is perpendicular to the transition boundary, i.e., perpendicular to bathymetric contours.  The wave is propagating in a direction that coincides with its wavenumber vector \underline{\textbf{K}}_1.  This direction is at an angle \theta_1 with the normal line.

As the wave crosses into shallower water, the phase speed decreases. Since this means that the wavelength gets smaller, the length of the wavenumber vector must get larger. At the boundary, the distance between crests in the y-direction (i.e. along the boundary line) is 2 \pi / l.  Since lines of constant phase (i.e, crests and troughs) have to match at the boundary, then this distance cannot change, i.e., l is a constant. This means that k must increase, resulting in a change in the angle that the wavenumber vector makes with the normal line.  Since  k  gets larger while l stays the same, \theta_2 < \theta_1, the wave travels in a new direction that makes a smaller angle with the normal line.  We describe this closer alignment between the direction of propagation and the normal line informally as “bending toward the normal”.  We can mathematically relate the two angles as follows, starting with the necessity that the distance between crests along the boundary is the same:

    \[ l_1 = l_2 \]

Using trignometry,

    \[ \vert \underline{\textbf{K}}_1 \vert sin{\theta_1} = \vert \underline{\textbf{K}}_2 \vert sin{\theta_2} \]

    \[ \frac{sin{\theta_2}}{sin{\theta_1}}=\frac{\vert \underline{\textbf{K}}_1 \vert}{\vert \underline{\textbf{K}}_2 \vert}, \]

Since frequency is constant, \omega=\omega_1=\omega_2,

    \[ \frac{C_2}{C_1}=\frac{\omega/\vert \underline{\textbf{K}}_2 \vert}{\omega/\vert \underline{\textbf{K}}_1 \vert}=\frac{\vert \underline{\textbf{K}}_1 \vert}{\vert \underline{\textbf{K}}_2 \vert}, \]

Key Takeaways

And so we end up with Snell’s Law,

    \[ \frac{sin{\theta_2}}{sin{\theta_1}}=\frac{C_2}{C_1}, \]

 

 

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book