31 Angular momentum on a rotating planet

In introductory mechanics you studied the conservation of angular momentum for simple solid bodies that are rotating. The angular momentum () about a given axis of rotation is defined by the product of the moment of inertia () and the rotation rate around that axis (, in radians per second).

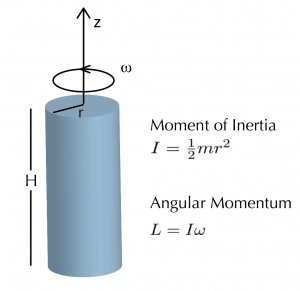
Angular momentum will change if a torque is applied to the system. Otherwise, it is a conserved quantity. The moment of inertia is related to how mass is distributed with distance from the axis of rotation (see the example moment of inertia for a cylinder in the figure). Changes in this distribution of mass will result in a change to the rate of rotation. A familiar example is that of a skater (perhaps modeled as a solid cylinder), that pulls their arms inward (thus decreasing the radius of the cylinder), in order to increase their spin rate.

On normal room-sized scales, say less than 1 km, the fact that the planet is also rotating can be ignored.  However, for water parcels in the ocean moving slowly over tens to thousands of kilometers, we must also take into account changes in planetary angular momentum. A water parcel changes planetary angular momentum by moving toward or away from the poles, because it the moves closer to or further from the axis of rotation of the Earth. The existence of a planetary contribution allows for a new, rather non-intuitive behavior. In order to conserve angular momentum, a water parcel may either change its local rate of spin (relative to the planet) or it may change its latitude.

In fluid mechanics, we use vorticity (, “zeta” = 2 times “omega”) to quantify the rate of spinning. We will now extend the definition of vorticity to include the contribution from planetary rotation. Because the ocean is a very thin layer of fluid in the planetary scale perspective, we will only be concerned about the component of vorticity in the local vertical direction, representing fluid rotation in the local horizontal plane.

At the pole, the planetary vorticity is , where (or radians per second), is the rate the Earth rotates about its axis. We have switched now to a capital “omega” since this is a constant not a variable. At the equator, the planetary vorticity is zero because the local vertical direction is perpendicular to the axis of Earth’s rotation. In between, it is given by the trigonometric relationship between the local vertical direction and the Earth’s rotational axis. At any point on the surface of the Earth, the Coriolis parameter is the name we give to the planetary vorticity in the local vertical direction,

where is latitude. We add the planetary vorticity, f, to the vorticity relative to the rotating reference frame, , defined as the curl of the horizontal velocity vector. We will now call the relative vorticity.

However it is not the total rotation rate that is a conserved quantity, but the total angular momentum.  Imagine a cylindrical water parcel in the interior of the ocean aligned with the local vertical axis, as sketched above.  Its volume is the surface area of the horizontal face times the height, . Because the 3D velocity is nondivergent, the volume is constant. Its moment of inertia can be written as . The angular momentum (per unit mass) of this water parcel is

In the last expression we have pulled all of the constants in the problem out front.  The remaining quantities that may vary for the water parcel are its latitude (affecting f), its relative vorticity (), and its vertical thickness (H).