30 Turbulence and vorticity

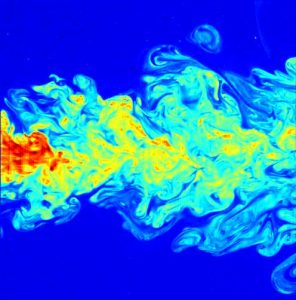
Energetically, turbulence transfers kinetic energy from larger to smaller spatial scales, by breaking up motions on the scales of ocean basins (thousands of km) into into motions on the scale of eddies (tens to hundreds of km) all the way down to the millimeter scale where the Reynolds number becomes small, and viscosity can finally dissipate the kinetic energy of macroscopic fluid motion into the random motion of molecules (heat). We will not study the physics of turbulence in detail in this course (one could take an entire course on this subject!).  We will only study force balances where turbulence is weak, or where its effects can be modeled as a simple diffusive flux of momentum or properties down their large-scale gradients (Fick’s Law, with a larger turbulent diffusivity).

Here, we will briefly describe the qualities of turbulence. It is characterized by:

• random, chaotic fluctuations in velocity and properties
• a lack of predictability
• the presence of vorticity across a wide range of space scales

We have not discussed vorticity yet.  Vorticity is defined as the curl of the velocity vector. It represents the swirling part of the velocity field. In fluid mechanics, vorticity is often given the symbol , but we will use because of later applications to large-scale oceanography.

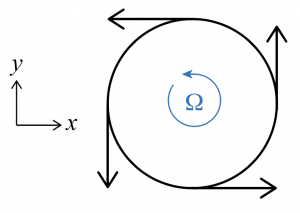
Let’s develop some understanding by thinking about the simple case of uniform circular motion in a horizontal plane. Recall that the speed that a particle moves around the axis of rotation is given by the product of the rotation rate (, in radians per second) and the distance from the axis of rotation (r), .

We can calculate the vorticity from the spatial field of velocity vectors, which do not change in time.

The magnitude of the fluid vorticity is just twice the rotation rate. The direction of the vorticity vector is along the axis of rotation (perpendicular to the plane of circulation motion), according to the right-hand rule and the sign of .

It is the development of vorticity that gives a turbulent fluid a swirling, eddy-filled nature, allowing for the more rapid transfer of properties through space than in a quiescent, laminar flow.