54 Acoustic waves in the ocean
Seawater is slightly compressible, and any disturbance in the ocean will create net inward or outward excess pressure forces on water parcels, tending to compress or decompress them, respectively. Water has strong resistance to compression, creating a restoring force that opposes this tendency with a very fast response time scale (tiny fractions of a second!). Thus, for the purposes of the environmental fluid mechanics on longer timescales that we have studied for most of the quarter, we have ignored water’s slight compressibility. However, these transient compressions and decompressions lead to longitudinal waves that propagate through the water at the speed of sound (the phase speed of the acoustic wave). For a nice animation of a longitudinal acoustic wave, see Dan Russell’s website Longitudinal and Transverse Motion.
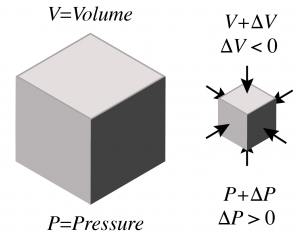
In a state of equilibrium, a water parcel experiences inward forces from its neighboring water parcels, i.e., the fluid pressure, P. In order to compress a fluid parcel, a small increase in net inward pressure is required, ![]() . This will lead to a slightly smaller volume
. This will lead to a slightly smaller volume ![]() , where
, where ![]() , and a small increase in density
, and a small increase in density ![]() .
.
The amount of excess pressure required to produce a given change in density is a characteristic of the medium. As we will see, it will turn out to be related to the sound speed, so we will anticipate that by using the symbol, C,
![]()
For small changes in volume,
![]()
Physically, this means that when ![]() (volume decreases),
(volume decreases), ![]() (density increases).
(density increases).
We can write
![]()
This equation is a linear relationship between force and spatial displacement (in 3D), an acoustic version of Hooke’s Law. Compression leads to an increase in local pressure, which creates an outward PGF – a restoring force. If we make the changes a continuous function of time, we get
![]()
Now we recognize that changes in volume are created by convergences or divergences of the velocity of the sidewalls,
![]()
To build intuition, let’s simplify to the situation shown in Dan Russell’s animation, where the motion only occurs in the x-direction. The acoustic Hooke’s law becomes
![]()
Our fluid still has to satisfy the fluid equivalent of Newton’s Law,
![]()
and we combine these equations by taking the time derivative of the first one and the x derivative of the second one, to find
![]()
This is an equation that can be solved by a function with the form of a propagating wave with ![]() . For this reason it is called the wave equation. To solve both equations, there also needs to be a particular relationship between pressure and velocity,
. For this reason it is called the wave equation. To solve both equations, there also needs to be a particular relationship between pressure and velocity, ![]() .
.
Media Attributions
- AcousticHookesLaw © Susan Hautala is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license

