26 Friction in a fluid

We will now consider the fluid equivalent of the other key contact force – the friction force – in a fluid.  The most common mathematical model is that the momentum concentration (aka, the velocity) diffuses down the gradient, a process analogous to Fick’s Law for properties.  Because of historical development, when this idea is applied to momentum it is called Newton’s Law of Viscosity.

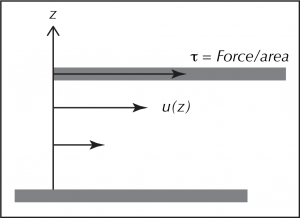
Consider a parallel velocity field between two plates, one that is fixed and one that is moving, as in the figure below. There is a constant rate of change of velocity within the fluid from zero at the fixed plate to a value that matches the speed of the moving plate at the top. This gradient of a component of velocity in a perpendicular direction, in this case is called shear.

Because of frictional contact forces, fluid parcels near the top are gaining momentum from the moving plate. Fluid parcels near the bottom are losing momentum to the stationary plate. Each fluid parcel in the interior is gaining momentum from its faster neighbor above, and losing momentum to its slower neighbor below. This means that there is a downward flux of momentum throughout the fluid, in a direction opposite to the vertical component of the gradient of .  Our “Fickian” model states that the magnitude of this flux is proportional to the shear, with the constant of proportionality, , called the momentum diffusivity, or viscosity.

 In the figure, since the velocity gradient is the same at the top and bottom, there is no convergence of the diffusive flux of momentum, and thus no acceleration.

However, to maintain this steady state, i.e., to keep the top plate in motion in the presence of friction, a force must be applied to it. There is an equal and opposite force from the bottom plate (the sum of the forces is zero). Intuitively, we think of the stationary bottom plate as “dragging” the fluid in a direction opposed to the motion of the top plate, with zero net force on the system, but a steady transfer of momentum downwards.