43 Propagating Waves (2D)
Water waves that propagate in two dimensions (horizontal), have a surface displacement can be represented by a similar function of the form
![\[ \eta(x,y,t) = Acos(kx+ly-\omega t), \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-aa4d2335a34e153b220d41369e895541_l3.png "Rendered by QuickLaTeX.com")
where we have set the phase shift constant 
for simplicity.
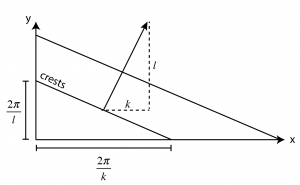
The wavenumber vector
![\[ \underline{\textbf{K}}=(k, l) \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e54e66dffdb570f8529a05e25eb675a0_l3.png "Rendered by QuickLaTeX.com")
is oriented perpendicular to lines of constant phase (i.e., wave crests and troughs) and indicates the direction the wave is propagating through space.
The wavelength, 
, is related inversely to the magnitude of the wavenumber vector,
![\[ \lambda = \frac{2 \pi}{\vert \underline{\textbf{K}}\vert} \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7cb125ff5529d41cd1ae49f008dc3465_l3.png "Rendered by QuickLaTeX.com")
Note that the wavelength is not a vector, in the sense that the distance between crests along the x-and y-axes are not its components. In fact, the distances between crests along the coordinate directions are generally longer than the distance along the perpendicular between wave crests.
This geometry also means that crests travel along the x- and y- axes at a rate that is larger than the rate crests travel in the direction of propagation. But we can still define an “apparent” phase velocity vector that indicates the rate that crests and troughs travel through space along each coordinate direction.
![\[ \underline{\textbf{C}}_{phase} = \left(\frac{\partial x }{\partial t},\frac{\partial y }{\partial t} \right) = \left(\frac{\omega }{k},\frac{\omega }{l}\right)\]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3ade7bb5fbf806dc8724fbbd053c0f67_l3.png "Rendered by QuickLaTeX.com")
A third component can be added to the wavenumber vector for wave propagation in three dimensions, but we will not consider such waves in this class.
Media Attributions
- WavenumberVector © Susan Hautala is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
