61 Absorption

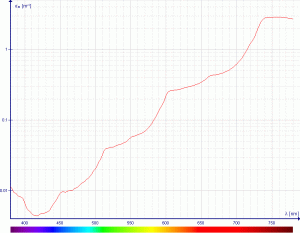
Here, we will not consider the detailed physics behind wavelength-dependent absorption, but an excellent summary can be found in the Ocean Optics Web Book article by Collin Roessler and Curtis Mobley. We will start with the fact that molecules, such as water, and photosynthetic pigments, absorb light in specific wavelength ranges.

Let’s quantify the absorption of light as it enters the ocean, directed downward. The fraction of light absorbed for a given distance (also called the path-length), , is called the absorbance (). As light continues deeper into the ocean, more and more is absorbed. The absorbance per meter of material (or, in our case, seawater) is called the absorption or attenuation or extinction coefficient, (sometimes written instead as ).

This leads to a differential equation,

that is solved, for constant , by the exponential function (try it!),

Thus, there is an exponential decay in energy flux (aka the intensity, or irradiance as it is often called in this context) moving deeper below the surface of the ocean (), with a decay-scale given by . The absorbance is . The transmittance, , is the fraction of initial energy flux remaining at a given depth, so

.

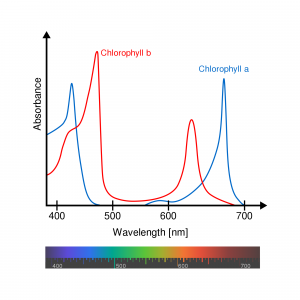
In a complex situation like the upper ocean, we define a bulk absorption coefficient based on the relative concentration () of its various constituents, including phytoplankton.

This is a form of what is more generally called the Beer-Lambert Law.  Measurements of the transmittance will yield estimates for the bulk absorption coefficient.

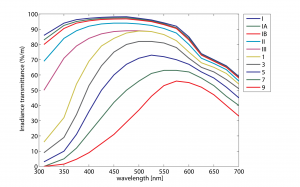
Bulk transmittance as a function of wavelength has been measured empirically in many different parts of the ocean. Water types are often classified according to their optical properties. Perhaps the most common of these classifications historically have been the Jerlov water types, as shown below in a figure from that section of the Ocean Optics Web Book.