63 The planetary energy balance

Climate predictions are based on complex whole Earth system models. However, at the heart of these models is the principle that the thermal emission from a planet must balance the incoming solar radiation, or the temperature of the planet will change until it does balance. We can gain understanding of this concept with relatively simple equations based on the Blackbody Radiation Laws.

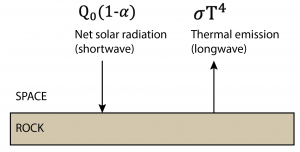
For a planet without an atmosphere, the equilibrium temperature must be such that the outgoing thermal emission is equal to the net incoming solar radiation (i.e., the amount that is not reflected back into space). , the albedo, quantifies the fraction of solar energy () that is reflected, so the net solar radiation transmitted into the materials of the planet is . Since the amount of energy these materials radiate back into space is a function of their temperature, the overall energy balance is

where is the average temperature of the planet. Now, let’s insulate the earth with a very simple representation of an atmosphere – a single layer of material that absorbs only long-wave radiation, establishing an equilibrium temperature that determines its thermal emission. This model is analogous to the glass roof of a greenhouse, hence the name greenhouse effect. We will consider two nested control volumes below two different altitudes, with each control volume needing to balance incoming and outgoing energy fluxes. The atmospheric thermal emission flux points in all directions, although only the vertical direction is relevant to the overall control volume balance.

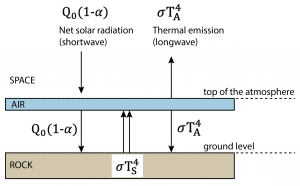
(1) Control volume = the planet below the level of the outer atmosphere. The balance is similar as above, and determines the temperature of the top of the atmosphere.

(2) Control volume = the planet below ground level. For simplicity, we assume that the atmosphere absorbs only long-wave radiation, i.e., it is transparent to incoming shortwave radiation. This means that the downward flux of solar radiation at ground level is the same as the downward flux at the top of the atmosphere,

Since it needs to balance both the downward solar radiation at short wavelengths, and downward thermal emission from the atmosphere, There will be a temperature gradient through the atmosphere.

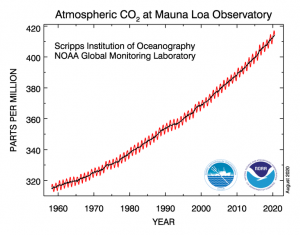
This oversimplified example is not particularly useful for actually predicting climate, but it does help us understand that the temperature at ground level depends on how the atmosphere absorbs both incoming shortwave and outgoing longwave radiation, qualities that depend on its mix of gases.  Particularly relevant for climate studies are the greenhouse gases, given this name because they have absorption bands in the infrared – the emission wavelength band of the Earth’s surface materials. Observed recent increases in the concentration of greenhouse gases, particularly carbon dioxide, have been linked to the rapid release of carbon previously stored in rock via the burning of fossil fuels.