11 The Continuity Equation
Imagine some volume interior to the ocean surrounded by imaginary sidewalls. We will call this a control volume, and develop conservation equations for water and properties of water inside it.
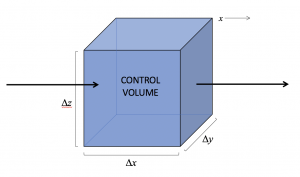
First, let’s think about the water itself. Recall that the flux of water is simply the fluid velocity.
There cannot be a net transport of water into a control volume, unless compression occurs, such that more mass takes up the same volume. But, at least on large scales, water is incompressible. Therefore, if an amount of water flows in through one part of the surface surrounding a control volume, then an equal amount must flow out through another part of the surrounding surface.
Since there is no net flux across the sidewalls, there is (by the divergence theorem) zero total divergence of the flux of water inside the control volume. If we imagine shrinking our control volume down to infinitesimal side, we write the equation:
![]()
This is called the continuity equation. Continuity in math means that variations have no discontinuities or singularities. Physically, we interpret the phrase to mean that water is not created or destroyed within the control volume.
Media Attributions
- ControlVolume © Susan Hautala

