10 The Curl, and Vorticity

The third of our important partial differential operations is taking the curl of a vector field.  This produces another vector.

We are only going to be concerned with the curl of a two-dimensional vector field in the horizontal plane in this class.  One important example is the curl of the horizontal velocity which is the definition of vorticity, commonly written as or (we will use ).  Since the z-component is zero in this case, we see that the vorticity only has a vertical component.

Physically, the vorticity is a metric of the local spinning motion of a fluid, in this case around the vertical axis.  The sign of the vorticity relative to “Up” follows the right-hand rule: if you wrap your fingers in the direction of the circulation of the vectors in the horizontal plane, your thumb will point in the direction of the curl vector in the vertical plane.

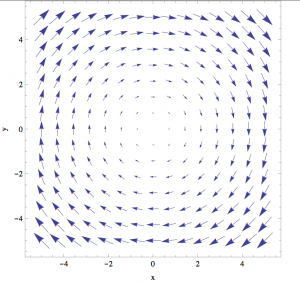
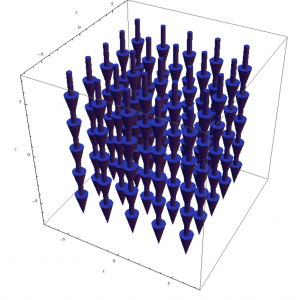
As an example, imagine the North Pacific subtropical gyre, a clockwise circulation in the horizontal plane (see figure below). To wrap your fingers in a clockwise manner (in the horizontal plane) with your right hand, your thumb must point downward.  Thus the large-scale curl of velocity here (its “vorticity”) is negative.

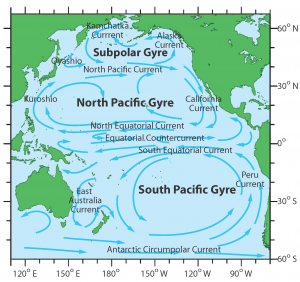
Notes:

• There is a fundamental theorem for curl that is analogous to the Divergence Theorem that you will learn about if you take Multivariate Calculus.  It is called the Circulation Theorem.  But we won’t go there in this class.
• For a highly visual discussion of curl see the second half of this YouTube video (you watched the first half in the last chapter):