2 Scalar and Vector Fields
A field in physics is a function that has a value at every point in space and time. One example is the gravitational field of the Earth. All of the variables we will use in this class are fields.
Using our convenient local Cartesian coordinate system, a scalar field has only a magnitude. Its value is a single number at any point in space, and time.
Important Scalar Fields in Oceanography
Some scalar fields in oceanography (scalar functions of the coordinates):
- Salinity, written mathematically as S(x,y,z,t), usually in parts per thousand or equivalent
- Pressure, P(x,y,z,t), in units of Force/Area (i.e., Pascals)
- Concentration of a dissolved substance, C(x,y,z,t), in various units
- Heat (q), obtained from temperature (T) by multiplying it by fluid density (
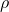, Greek letter “rho”) and heat capacity (Cp)
![\[ q(x,y,z,t) = \rho C_p T(x,y,z,t) \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3f6e767e2b1c9024bd049afd8e98d2a7_l3.png "Rendered by QuickLaTeX.com")
Heat has energy units (i.e., Joules).
A vector field has a three-dimensional vector at every point in space and time. Imagine space filled with small arrows with a direction and magnitude (length) that vary with spatial location, and also change in time.
Important Vector Fields in Oceanography
Three important vector fields in oceanography:
- The fluid velocity, written as u(x,y,z,t) has components (u, v, w) in each coordinate direction
- The flux of substance C, written as FC(x,y,z,t)
- The pressure gradient force, written as FP(x,y,z,t)
Review Material (hopefully these are blasts from your past):
- While a scalar has only a magnitude, a vector has both magnitude and direction.
- Vertical bars surrounding a vector indicate its magnitude.
- To calculate the magnitude of a vector: sum up the squares of the components, then take the square root of the total. For example, speed is the magnitude of the velocity vector. You would write it as:
![\[ \lvert \underline{\textbf{u}} \rvert = \lvert (u,v,w) \rvert =\sqrt{u^2+v^2+w^2}= \left( u^2+v^2+w^2 \right)^{1/2} \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-658f84828a15a491dee9488e287281f0_l3.png "Rendered by QuickLaTeX.com")
