15 Advection-Diffusion Equation

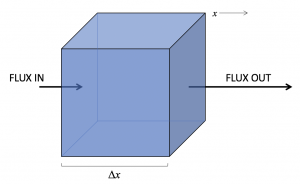
Sketch of a positive flux divergence contribution from changes in the x-direction, associated with more transport leaving the control volume than transport entering.

Finally, we are going to build on our previous work to develop a conservation equation for a substance subject to both advection and diffusion. We start with our previous equation for the change over time of concentration in a control volume (in words: the rate of change of concentration can be found from the divergence of the flux of that substance, times minus one):

    \[{ \frac{\partial C}{\partial t}} =-\nabla \cdot \underline{\textbf{F}}\]

In the figure above, the flux divergence is positive (more of the substance is leaving than entering) and so we expect the concentration in the box to decrease.

Next we add contributions from both advective and diffusive flux divergence, using the expressions we have derived:

    \[{ \frac{\partial C}{\partial t}} =-\nabla \cdot \underline{\textbf{F}}_{Advective} -\nabla \cdot \underline{\textbf{F}}_{Diffusive} = -\underline{\textbf{u}} \cdot \nabla C + K \nabla^2 C \]

The above equation works for a conservative property in the ocean, where conservative means no interior sources or consumption (called “sinks”) of the property.  An example of a conservative property is salinity. If there are sources or sinks, as there are for many important substances such as carbon, oxygen, or nutrients, then that can be added to the right side of the equation. It is added there as a source term since a positive value results an increase in concentration over time.  A negative source would indicate that there is consumption of the substance within the interior of the ocean.  The source may also vary in time and space.

Key Takeaways

The advection-diffusion equation for a substance with concentration C is:

    \[{ \frac{\partial C}{\partial t}} = -\underline{\textbf{u}} \cdot \nabla C + K \nabla^2 C + Source(x,y,z,t) \]

This form assumes that the diffusivity, K, is a constant, eliminating a \nabla K \cdot \nabla C term. While valid for molecular diffusion, the assumption does not work all that well for turbulent diffusion, but we will use the simpler expression above in this class in order to develop basic understanding.

If we expanded the equation in the box above it would be:

    \[{ \frac{\partial C}{\partial t}} = -\left(u \frac{\partial C}{\partial x}+v \frac{\partial C}{\partial y}+w \frac{\partial C}{\partial z}\right) + K \left(\frac{\partial^2 C}{\partial x^2}+\frac{\partial^2 C}{\partial y^2}+\frac{\partial^2 C}{\partial z^2}\right) + Source(x,y,z,t) \]

 

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book