"

38 Ocean Gyre Circulation

At every point in space, Sverdrup balance gives us a quantitative relationship between the sign of the wind-stress curl and the sign of the geostrophic transport in the upper ocean. Since the wind-stress curl is negative over the entire subtropical gyre, this means that there will be net southward geostrophic transport in the ocean. But, in order to conserve mass, there must be northward return flow that is equal and opposite to the Sverdrup transport across every latitude. This return flow can only happen in a narrow boundary layer, where the flow can have a substantial ageostrophic component. For reasons discussed in the next section, this boundary layer is located on the western side of the ocean basin.

The existence of the return flow implies the existence of gyre circulation.  For example in the subtropics, there is southward flow in the interior that recirculates northward in the western boundary current, setting up a clockwise circulation in the northern hemisphere, called an anticyclonic gyre.  To calculate the southward transport in the interior, we integrate the y-component of geostrophic velocity from an arbitrary point x to the eastern boundary, located at x = x_{East}.

    \[ \frac{\beta}{f}\int_x^{x_{East}}Transport_{Geostrophic}^y dx = \frac{1}{\rho_0} \int_x^{x_{East}}\nabla \times \left( \frac{\underline{\tau}_{WIND}}{f} \right) dx\]

Idealized interior ocean gyre transport in response to a wind stress field that varies sinusoidally with latitude. The left panel shows a plot of wind stress as a function of latitude with maximum negative values corresponding to the trade winds at the equator and maximum positive values corresponding to the westerlies at 40°N. The right panel shows contours of transport (ranging from 0 to 55 Sv), integrated between the longitude of the contour lines and the eastern boundary.
Sverdrup transport for an idealized rectangular subtropical Northern hemisphere ocean basin integrated between point x and the eastern boundary (in Sv, 1 Sv = 1 million cubic meters per second). The idealized wind-stress only depends on latitude, as shown at the left. The Sverdrup transport is contoured in 5 Sv increments.

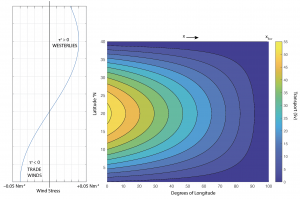
Each contour line represents an increment of transport.  For example, there are 5 Sv flowing around the gyre between the 10 and 15 Sv contours.  The flow follows the contours, and the x-component of the transport can be found using the angle of these transport streamlines with the x-direction, although we will not develop that quantitative expression in this class.

Mini-lecture for class:

Media Attributions

  • SverdrupTransport © Susan Hautala

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book