24 Streamlines

We have just discussed potential energy and are moving toward an equation for energy conservation in a fluid. But first, we need to discuss a diagnostic for water parcel pathways called streamlines. Streamlines are constructed as a family of curves that are everywhere tangent to the velocity vector, and thus the direction of water parcel motion is always along streamlines. These streamlines are lines of constant values of the streamfunction.  The streamfunction, \psi is defined by solving:

    \[ u=\frac{\partial \psi}{\partial y}\qquad v=-\frac{\partial \psi}{\partial x} \]

The minus sign can appear in either equation, as long as u and v have opposite signs, but the version above is traditional for non-rotating fluid mechanics.

 

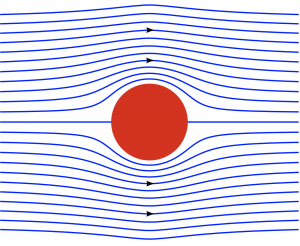
An example for the streamlines of flow around a cylinder – imagine that this is a horizontal slice through a cylinder standing vertically in a fluid flowing from left to right.  This is the solution for steady flow in the absence of friction.

Key Takeaways

Looking at contour plots of the streamfunction for steady flow helps us build a mental picture of it because:

  • Streamlines (lines of constant streamfunction) are identical to water parcel trajectories
  • When streamlines are closer together, the flow speed is faster

In the example above, we can see regions of faster flow (more closely packed streamlines) on either side of the cylinder where the flow diverts around it and speeds up, and regions of slower flow (less closely packed streamlines) on the cylinder’s upstream and downstream sides.

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book