46 Wave energy flux

We are interested in the question of how much of the energy of a wave is reflected or transmitted, and thus we need to consider wave energy.

Recall that work is defined as the change in energy, , of a system before and after some force is applied, and that .  Work has units of Joules.  The rate at which energy changes over time, or the power, is thus the rate of doing work, .  The rate of doing work has units of Joules per second, or Watts. Since velocity is the rate of change of distance with time, we can write the rate of doing work as .

For a fluid, we will consider the intensity, , defined as the power per unit area of a surface. Intensity is a vector and physically represents the wave energy flux through a surface in the direction of wave propagation.  It has units of Watts per square meter.  For the wave with an oscillation in both pressure (i.e., force per square meter) and velocity

where we have used, , to write the final expression in terms of the impedance.

Now, let’s consider a cosine oscillation in pressure, (i.e., the pressure oscillation as a wave passes through a point fixed in space).  We want to know if there is a net rate of working over the entire wave cycle.  We thus average over one period in time.  The average value of a squared cosine (or sine) function is (this is apparent in the graph, and can be shown mathematically but we will not do so here).

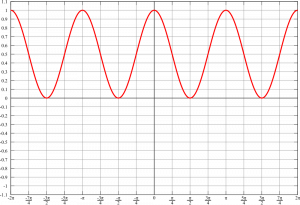
Thus the net rate of working (per unit area) over a wave cycle is

where the overbar indicates the average over one period.  Depending on the historical development of a particular application, just the word “intensity” can refer to either the maximum intensity reached during the wave cycle or its average, and this can lead to factors of two difference in metrics of intensity, so be a bit careful.