7 The Gradient
The gradient is a vector with a magnitude that quantifies the total amount of change of a field per unit change in distance. It points along the direction of the maximum change. The gradient is only defined for a scalar field. The operation of taking the gradient of a scalar produces a vector.
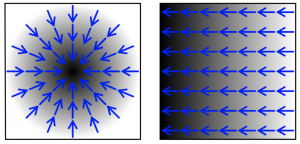
The easiest way to visualize this is with a two-dimensional gradient of concentration (a scalar) in a horizontal plane as in the figure below. In this figure, higher concentrations are shaded more darkly and the blue arrows show the concentration gradient vector field.
Key Takeaways
The mathematical definition of the gradient of the scalar field C (in our three standard spatial dimensions) is:
![\[ \nabla C = \left( \frac{\partial C}{\partial x}, \frac{\partial C}{\partial y}, \frac{\partial C}{\partial z} \right) \]](https://uw.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-acf1cce4723ec59a9ffecb8477ef026a_l3.png "Rendered by QuickLaTeX.com")
where we have used the partial derivative operator defined on a previous page.
For a highly visual discussion of partial derivatives and the gradient, see this YouTube video:
Media Attributions
- Gradient is licensed under a CC BY-SA (Attribution ShareAlike) license
