3 The Dot Product
In three-dimensional space, we often want to determine to component of a vector in a particular direction. We use a vector operator called the dot product. For two vectors ![]() , and
, and ![]() :
:
![]()
Geometrically the dot product gives the magnitude of the component of ![]() that is aligned with
that is aligned with ![]() , multiplied by the magnitude of
, multiplied by the magnitude of ![]() .
.
- If two vectors are perpendicular to one another, then the dot product is zero.
- If two vectors are parallel, then the dot product is
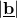 times
times 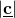 .
.
If ![]() is a unit vector with an arbitrary direction, then the dot product will give the component of
is a unit vector with an arbitrary direction, then the dot product will give the component of ![]() in that direction.
in that direction.
Examples
The dot product of the fluid velocity and one of the Cartesian coordinate unit vectors gives the current component in that direction. For example, let’s suppose that the current is 2.88 ms-1 to the northwest and upwelling at 0.01 cm s-1
![]()
![]()
gives the northward component of the fluid velocity.
There is another important vector operator called the cross product, but we will define that a bit later.
Want more info (optional)?

