9 The Divergence Theorem
The divergence theorem is an equality that can be proven for any vector field. All of our conservation equations and large-scale budgets that are so useful in oceanography are based on this mathematical principle. In this context, the vector field is the flux of some property in the ocean.
The divergence theorem relates the net transport outward through the surrounding surface of a closed volume to the total divergence inside. Consider the figure below showing vector field ![]() and the surface of a sphere. There is a positive divergence inside the sphere that results in outward directed flux vectors. In this particular illustration, the flux vectors along the surface are directed outward everywhere, but this is not necessary – there could be some inflowing vectors and some outward flowing vectors – what matters is the net transport, found by adding up “flux times area” elements over the entire surface.
and the surface of a sphere. There is a positive divergence inside the sphere that results in outward directed flux vectors. In this particular illustration, the flux vectors along the surface are directed outward everywhere, but this is not necessary – there could be some inflowing vectors and some outward flowing vectors – what matters is the net transport, found by adding up “flux times area” elements over the entire surface.
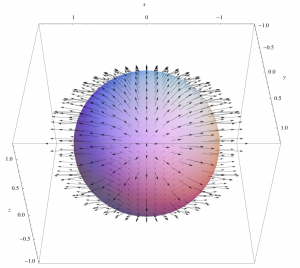
This theorem is usually stated mathematically using surface and volume integrals, but that is beyond the level of calculus expected for this class. Instead, we will approach it by imagining that the surface of the sphere is divided up into a very large number of surface elements.
The i-th surface area element:
- has surface area
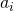 .
. - is associated with a local value of the flux vector
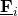
- has a unit normal vector
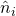 that is directed outward and perpendicular to this surface element
that is directed outward and perpendicular to this surface element - has an outward flux passing through the surface
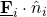
The total outward transport (flux times area) passing through the surface of the sphere = ![]()
Next, we apply a similar idea to the volume inside the sphere, dividing it up into a very large number of volume elements.
The j-th interior volume element:
- has volume
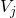
- is associated with a local vector
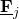
- is associated with a local divergence of that vector field
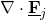
Key Takeaways
The divergence theorem sets the net transport outward across the surface of a closed volume (e.g., the sphere in the figure above) equal to the total divergence inside the sphere.
![]()
In words:
- The left side sums up the normal (outward) flow component multiplied by area for all sides.
- The right side is the average flux divergence inside the volume multiplied by the volume (technically, only for equally sized volume elements).
Practically, if there is a net outward transport of a property across some volume, there must be a source of that property inside the volume (in order for there to be a positive total divergence).
Mini-lecture for class:
Optional: For a highly visual discussion of divergence and the divergence theorem, see the first half of this YouTube video:
Media Attributions
- DivergenceTheorem © Glosser.ca is licensed under a Public Domain license

