Stratification and buoyancy forces

Susan Hautala

22 Stratification and buoyancy forces

If water parcels are not uniform in density, the state of rest is one where the fluid is stratified, i.e., water parcels with greater density sit below water parcels of less density.

Key Takeaways

There are a number of metrics for the strength of the stratification, the name given to the vertical component of the density gradient, $\partial \rho / \partial z$ . One of the most common is N, the buoyancy frequency (we will later talk about why it has this name), defined as:

$N = \sqrt{-\frac{g}{\rho_0}\frac{\partial \rho}{\partial z}}$

If a water parcel is displaced vertically away from its equilibrium position in a stratified fluid, then a force opposing this motion occurs, restoring the stratification. This force is called the buoyancy force.

Diagram for thinking about the vertical forces on a water parcel moving from 1 to 2 without changing its density

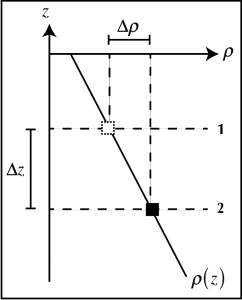
Mathematically, let’s consider two water parcels, WP1 and WP2 with densities $\rho_1 < \rho_2$ , in a linearly stratified fluid (i.,e., $\partial \rho / \partial z$ is a negative constant number). Move WP1 vertically down to the level where the fluid density is $\rho_2$ , without changing its density. This involves a change in depth of $\Delta z=z_2-z_1$ that is negative for a downward displacement.

From hydrostatic balance, the pressure gradient at the lower level is

$\frac{\partial P}{\partial z}= -\rho_2 g$

The net upward force on WP1 per unit mass of WP1 due to pressure forces from the surrounding fluid is

$-\frac{1}{\rho_1}\frac{\partial P}{\partial z}= \frac{\rho_2}{\rho_1}g$

Key Takeaways

The buoyancy force is defined as the sum of vertical forces (per unit mass) on the displaced water parcel. It includes gravitational acceleration.

$\sum F = \frac{\rho_2}{\rho_1}g - g = \frac{\rho_2-\rho_1}{\rho_1}g$

Thus, the buoyancy force on the displaced water parcel depends on the percentage of its density difference from the surrounding water.

In our linear stratification, or in a linear neighborhood of a general stratification assuming a small displacement, $\Delta z$ , the density difference is $\Delta \rho=\rho_2-\rho_1=(\partial \rho / \partial z)\Delta z$ . Thus, for a given displacement size, the strength of the buoyancy force depends on the strength of the water column stratification.

The buoyancy force can be seen to be closely related to our stratification metric, N, since density variations are small, $\rho_1 \approx \rho_0$ , and