66 Dynamic height and horizontal pressure gradients

Let’s start by thinking about the horizontal pressure gradient, but where the numerator uses pressure differences taken along an arbitrary surface (s) that can vary in height.  The values along the surface will change by an amount equal to changes along constant z surfaces (the regular Cartesian horizontal gradient), plus an amount that has to do with how the z-value of that surface changes given an existing vertical component of pressure gradient.

Sketch illustrating differences between pressure gradients along z = constant and an arbitrary surface, s = constant.

    \[ \frac{\partial P}{\partial x}\biggr|_s =\frac{P_3-P_1}{\Delta x}=\frac{P_2-P_1}{\Delta x}+\frac{P_3-P_2}{\Delta x}=\frac{P_2-P_1}{\Delta x} + \frac{\partial P}{\partial z} \frac{\Delta z}{\Delta x} \]

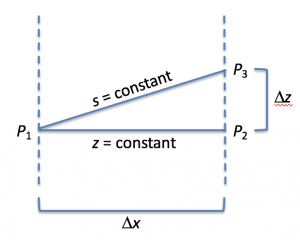
This is formally related to a chain rule expansion of a partial derivative taken where s is a coordinate. In the expression below, the subscript on the vertical line means “keeping that variable constant”.

    \[ \frac{\partial P}{\partial x}\biggr|_s =\frac{\partial P}{\partial x}\biggr|_z+\frac{\partial P}{\partial z}\biggr|_x \frac{\partial z}{\partial x}\biggr|_s \]

Now, consider that the surface in question is a pressure surface, recognizing that constant P surfaces are not always aligned with constant z surfaces in an ocean that is not at rest. The term on the left will be zero since the change in pressure along a constant pressure surface is by definition zero.  Thus, the two terms on the right must sum to zero, requiring:

    \[ \frac{\partial P}{\partial x}\biggr|_z =-\frac{\partial P}{\partial z}\biggr|_x \frac{\partial z}{\partial x}\biggr|_P \]

Now consider the difference in horizontal pressure gradient at two different points in the water column where the pressures are, respectively, P1  and P2 and the heights are, respectively z1 and z2. If we also assume that density changes are a small percentage of the full density such that \frac{\partial P}{\partial z}=-g\rho_0 at all depths then

    \[ \frac{\partial P}{\partial x}\biggr|_{z_2}-\frac{\partial P}{\partial x}\biggr|_{z_1}=g\rho_0 \left(\frac{\partial z}{\partial x}\biggr|_{P_2}-\frac{\partial z}{\partial x}\biggr|_{P_1} \right) \]

If we then divide through by -\rho_0, the left side becomes the difference in PGF (pressure gradient force) = –\frac{1}{\rho_0}\frac{\partial P}{\partial x} at the two levels.

    \[ PGF_{z_2}-PGF_{z_1}=-g \left(\frac{\partial z}{\partial x}\biggr|_{P_2}-\frac{\partial z}{\partial x}\biggr|_{P_1} \right) \]

The right side is the horizontal gradient in the geopotential difference (gz2-gz1) along constant pressure surfaces, which are related to dynamic height via its definition

    \[ D=-\int_{P_1}^{P_2}\frac{1}{\rho}dP=g\left( z_2-z_1 \right)\]

Thus

    \[ PGF^x \vert_{z_2}-PGF^x \vert_{z_1}=-\frac{\partial D}{\partial x} \]

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book