"

20 Hydrostatic balance

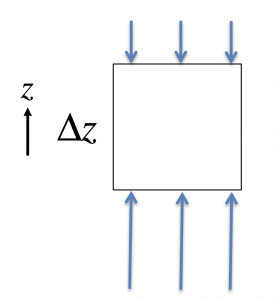
Sketch of a control volume with the z-axis indicated pointing upward and a length delta-z along this axis. Longer vectors point upward at the bottom surface of the control volume, indicating greater pressure than at the top where shorter vectors point downward.
Schematic for hydrostatic balance, i.e. a vertical force balance between the gravitational acceleration, g, and the vertical components of the PGF.

We know from experience that pressure increases with depth in the ocean, but why? Consider a water parcel (an infinitesimal control volume) in the ocean interior.  Because pressure is increasing with depth, there will be a greater total force on the lower surface than on the upper surface, associated with a net upward PGF.

Why don’t water parcels accelerate upward in response to the PGF? In the ocean there is a steady-state balance between the vertical component of the PGF and the downward-directed gravitational acceleration (-g=-9.81 m s^{-2}, the gravitational force per unit mass) that keeps water parcels in the ocean close to a state of zero vertical acceleration.

This balance can be written, with the acceleration (0) on the left, and forces on the right:

    \[ 0=PGF+\frac{gravitational force}{mass} \]

    \[ 0=-\frac{1}{\rho}\frac{\partial P}{\partial z}-g. \]

We can thus calculate the vertical pressure gradient

    \[ \frac{\partial P}{\partial z}=-\rho g. \]

Since the right side is always a negative number, pressure decreases as we move upwards (to greater values of z) within the ocean.

By integrating this expression from some depth below the resting ocean surface, z=-H, to the sea surface, z=0, we can find the hydrostatic pressure at depth H.

    \[ \int_{-H}^0 \frac{\partial P}{\partial z} dz=P(0)-P(-H)=-\rho g \left. z \right]_{-H}^{0} . \]

Oceanographers commonly use a convention that the atmospheric pressure P(0)=0, thereby wrapping the standard atmosphere into the background state. The pressure at depth H (where z=-H) becomes

    \[ P(-H)=\rho g H. \]

If you are not yet familiar with integration, you can instead think of a finite difference representation of the gradient over a small distance,

    \[ \frac{\partial P}{\partial z} \approx \frac{\Delta P}{\Delta z}=\frac{P(0)-P(-H)}{0-(-H)}=-\rho g, \]

and you will end up with the same expression when you solve for P(-H).

Key Takeaways

Hydrostatic Balance is the state where the gravitational acceleration balances the vertical component of the pressure gradient force.

In a resting fluid with the sea surface at z = 0, the value of the hydrostatic pressure at depth H (where z=-H) is

    \[ P(-H)=\rho g H. \]

The hydrostatic pressure gradient has only a vertical component, equal to

    \[ \frac{\partial P}{\partial z}=-\rho g. \]

Note: In general, if the ocean is not at rest, then its surface may not be located at z=0. You would still use the depth below the ocean surface, H, but the z-coordinate at that depth may vary.

Mini-lecture for class:

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book