"

34 Geostrophic shear

Since the pressure gradient can change with depth, the geostrophic current can change with depth.  The vertical gradient of the geostrophic velocity is called the geostrophic shear. The diagram below shows a horizontal gradient in hydrostatic pressure that changes with depth due to a sloping surface of constant density, also called an isopycnal.

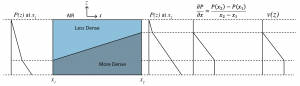
Colored panel showing a sketch in the xz-plane of less dense water above more dense water with an interface that slopes upward to the right. The example is in the northern hemisphere. x1 is the coordinate of the left edge and x2 is the coordinate of the right edge. Various quantities are then plotted as a function of depth: (1) Pressure as a function of depth at x1 showing a shift to a higher rate of pressure increase with depth in the denser layer; (2) The same at x2, but showing that the shift occurs at a shallower depth due to the sloping interface; (3) The pressure gradient (= delta-P divided by delta-x) showing zero pressure gradient above the depth where the sloping interface intersects x2, an increasing pressure gradient in the depth range of the sloping interface line and then constant pressure gradient below the point where the interface line intersects x1; (4) The geostrophic velocity associated with this pressure gradient showing zero velocity above the depth where the sloping interface intersects x2, northward flow that increases with depth, in the depth range of the sloping interface line, and then constant northward flow below the point where the interface line intersects x1.
The blue-colored diagram shows two fluid layers of different density with a sloping interface. The plots nearest this diagram show schematic hydrostatic pressure profiles at the left and right sides. Also shown are the pressure gradient as a function of depth and the corresponding geostrophic velocity (northern hemisphere assumed).

For the general case, where temperature and salinity vary continuously with depth, we can show mathematically that the geostrophic shear can be calculated from knowledge of just the density field.  For example, starting with the east-west geostrophic velocity,

    \[ u =- \frac{1}{f \rho_0 }\frac{\partial P}{\partial y}, \]

take the vertical derivative, and the swap the order of the partial derivatives to get

    \[ \frac{\partial u}{\partial z} =- \frac{1}{f \rho_0 }\frac{\partial }{\partial y}\frac{\partial P}{\partial z}. \]

Next substitute in the hydrostatic vertical gradient of pressure to find the geostrophic shear in the x-direction

    \[ \frac{\partial u}{\partial z} =\frac{1}{f \rho_0 }\frac{\partial }{\partial y}(g \rho)\]

A similar derivation can be applied to the y-component of geostrophic velocity.

Key Takeaways

The geostrophic shear is related to horizontal gradients of density. For reasons related to their historical development in the atmosphere, these equations are called the thermal wind equations:

    \[ \frac{\partial u}{\partial z} =\frac{g}{f \rho_0 }\frac{\partial \rho}{\partial y} \]

    \[ \frac{\partial v}{\partial z} =-\frac{g}{f \rho_0 }\frac{\partial \rho}{\partial x} \]

Notes:

  1. The appropriate density to use when calculating the geostrophic shear is the potential density
  2. If you are feeling uncomfortable about swapping the order of the 2nd partial derivative between the first and second equations above (this is called a “mixed partial derivative” by the way), see the 2nd partial derivative article from Khan Academy.

Mini-lecture for class:

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book