"

62 Thermal emission and blackbody radiation

Any material with a temperature above absolute zero will have oscillating charged particles and thus emit electromagnetic radiation, a process called thermal emission. For objects at room temperature, this radiation is in the infrared wavelength band. For objects as hot as stars, this radiation is in the visible and ultraviolet bands.

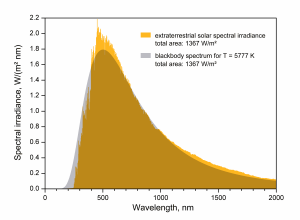
The theoretical and observed solar spectrum at the outer atmosphere. The x-axis shows wavelength ranging from 0 to 2000 nm. The y-axis shows the irradiance spectrum in Watts per meter-squared per nm. Colors show the observed data wit a peak at about 500 nm overlaid with the best-fit blackbody spectrum curve corresponding to absolute temperature, T = 5777 K. The total area under each curve is 1367 Watts per meter-squared.
The effective temperature, or blackbody temperature, of the Sun (5777 K) is the temperature a black body of the same size must have to yield the same total emissive power. The gray curve shows the Planck’s Law function for a body at this this temperature.

Theory exists for the intensity of the emitted radiation as a function of wavelength – the Blackbody Radiation Laws. The phrase “blackbody” may seem strange – it is meant to describe an object that absorbs all incoming radiation regardless of wavelength, i.e., there is no surface reflection. Planck’s Law specifies the theoretical function of wavelength for the thermal emission intensity from such a blackbody.

The Planck function has a prominent peak in the spectrum of emission intensity, with a temperature dependence that is given by Wien’s Law,

    \[ \lambda_{peak}=\frac{b}{T},\quad b=2.898 \times 10^{-3} m K. \]

As the units suggest, the temperature must be specified in degrees Kelvin (K) = degrees Celsius + 273.16.

The total energy flux is also temperature dependent. Integrated over all wavelengths the total emission intensity is given by the Stefan-Boltzmann Law,

    \[ Q = \sigma T^4, \quad \sigma=5.67 \times 10^{-8} W m^{-2} K^{-4}. \]

Below is an interactive calculator for the distribution of emitted energy as a function of wavelength – the Planck function – by PHET Interactive Simulations at the University of Colorado Boulder.

Mini-lecture for class:

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book