64 Changing Concentration related to Flux Divergence

Sketch of a positive flux divergence contribution from changes in the x-direction, associated with more transport leaving the control volume than transport entering.

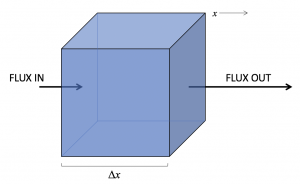
We will derive a relationship between the time rate-of-change of total amount of substance inside the control volume (Concentration times Volume) and the difference in transport across the sidewalls:

    \[ \frac{\partial}{\partial t}\left( C\times Volume \right)=Transport\hspace{3 pt}IN-Transport\hspace{3 pt}OUT \]

Since the volume does not change:

    \[ \frac{\partial C}{\partial t}\times Volume=Transport\hspace{3 pt}IN-Transport\hspace{3 pt}OUT \]

    \[ \frac{\partial C}{\partial t}\times \Delta x \Delta y \Delta z=Transport\hspace{3 pt}IN-Transport\hspace{3 pt}OUT \]

First, let us just consider the contribution to the total rate of concentration change due to the x-component of flux shown in the figure above.  Remember that transport is flux times area.  For the x-component of flux (F^x), the relevant face has area \Delta y \Delta z:

    \[{ \frac{\partial C}{\partial t}}\biggr|_1 \times \Delta x \Delta y \Delta z=\left(F_{IN}^x-F_{OUT}^x\right)\Delta y \Delta z\]

Now divide by the volume (the \Delta y \Delta z cancels out of the numerator and denominator on the right side):

    \[{ \frac{\partial C}{\partial t}}\biggr|_1 =\frac{F_{IN}^x-F_{OUT}^x}{\Delta x}\]

Now change the sign on the right so that the numerator represents a \Delta F in the direction of increasing x.  Then allow the control volume to become infinitesimally small so that the ratio of discrete changes in the x-direction can be represented by the continuous first partial derivative.

    \[{ \frac{\partial C}{\partial t}}\biggr|_1 =-\left(\frac{F_{OUT}^x-F_{IN}^x}{\Delta x}\right)=-\frac{\Delta F^x}{\Delta x}=-\frac{\partial F_x}{\partial x}\]

There are similar contributions due to variations of fluxes in the other two coordinate directions:

    \[{ \frac{\partial C}{\partial t}}\biggr|_2 =-\frac{\partial F^y}{\partial y}\]

    \[{ \frac{\partial C}{\partial t}}\biggr|_3 =-\frac{\partial F^z}{\partial z}\]

Add these all together for how the total time rate of change of concentration relates to the flux divergence:

    \[{ \frac{\partial C}{\partial t}} =-\left(\frac{\partial F^x}{\partial x}+\frac{\partial F^y}{\partial y}+\frac{\partial F^z}{\partial z}\right)=-\nabla \cdot \underline{\textbf{F}}\]

 

 

Media Attributions

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Physics Across Oceanography: Fluid Mechanics and Waves Copyright © 2020 by Susan Hautala is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book