21 Archimedes’ Principle

Now let’s think about the forces due to hydrostatic pressure that can arise when a water parcel is displaced vertically from its equilibrium position. We do this so that we can then understand the effects of density stratification.

You have likely heard of Archimedes’ Law, or Principle, which states that the net upward force on a floating or submerged object is equal to the weight of the water the object displaces. We can think of a water parcel as just a submerged object.

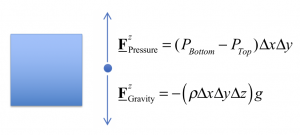
In hydrostatic balance, the force difference between the bottom and top surfaces (the net force) is equal to the weight of the water parcel.

You can understand the signs on the left side by remembering that the normal force at the bottom is directed upward (toward positive z) and the normal force at the top is directed downward. The right side is mass times gravitational acceleration, i.e., the weight of the fluid. This is a statement of Archimedes’ Law – if you imagine replacing the cubic volume above with a solid body, the pressure force from the fluid outside is equal to the weight of the replaced/displaced fluid.

Let’s reverse the order on the left and rearrange a bit.

if we divide through by the volume, and substitute for the vertical pressure difference, we recover the hydrostatic balance equation

So Archimedes’ Principle is just a macroscopic manifestation of hydrostatic balance in a fluid.