13 Advection and Diffusion
We have already talked about advective flux and its divergence. To summarize:
Key Takeaways
Advection is the process by which stuff is moved around by ocean currents. The advective flux of a substance, is the fluid velocity multiplied by the concentration, C:
![]()
Since the velocity has zero divergence, what is important to the advective flux divergence is how the concentration changes in space (the gradient), multiplied by the component of velocity in the direction of the gradient vector.
The advective flux divergence is:
![]()
Diffusion is the process by which larger scale gradients in a dissolved substance are eliminated over time through the random motion at the molecular scale. It is modeled according to Fick’s Law. The flux is proportional to the magnitude of the concentration gradient, and is directed opposite to the gradient. We often use the term directed “down the gradient” to describe this direction. Similarly a vector directed “up the gradient” would point in the same direction as the gradient vector.
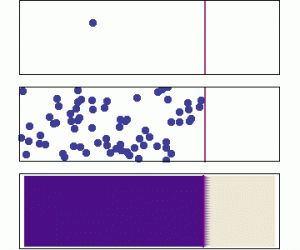
If the animation above does not play, click on it to open it in a new view (use the back arrow afterwards to return).
Key Takeaways
The diffusive flux is:
![]()
The constant of proportionality in Fick’s Law, K, is called the diffusivity.
If the diffusive flux on one side of a control volume is equal to the diffusive flux on the other side of the control volume (i.e., the gradient is the same), it will not affect concentration. To change concentration, there must be a divergence of the diffusive flux.
Key Takeaways
The diffusive flux divergence is:
![]()
where we have assumed that the diffusivity, K, is a constant. That assumption works fairly well for molecular diffusion.
This is often written using a shorthand notation with the operator ![]() which just means take the second derivative in each coordinate direction and add them together:
which just means take the second derivative in each coordinate direction and add them together:
![]()
The diffusive flux field has nonzero divergence only when the field has curvature (as indicated by the sum of the second derivatives). This is equivalent to saying that the gradient (the first derivative) is not the same everywhere in space.
Mini-lecture for class:
Media Attributions
- DiffusionMicroMacro © Sbyrnes321 is licensed under a Public Domain license

