Introduction

SIMPER is intended for comparisons among levels of a categorical variable, where the response matrix is expressed as a distance matrix, particularly the Bray-Curtis dissimilarity measure.

We will illustrate it using our oak example, and comparing compositions between the three levels of our Grazing factor.  See the beginning of this section for details about how to create these objects.

Bray-Curtis Dissimilarity

Recall that compositional data are often summarized using the Bray-Curtis dissimilarity measure:

[latex]D_{i,h} = \frac{\sum_{j=1}^p \mid a_{ij} - a_{hj} \mid} { \sum_{j=1}^p a_{ij} + \sum_{j=1}^p a_{hj} } = 1 - \frac{ 2 \sum_{j=1}^p MIN(a_{ij}, a_{hj}) }{ \sum_{j=1}^p a_{ij} + \sum_{j=1}^p a_{hj} } = 1 - \frac{ 2 \sum_{j=1}^p MIN(a_{ij}, a_{hj}) }{ a_{i\cdot} + a_{h\cdot} }[/latex]

where

• [latex]p[/latex] is the total number of species
• [latex]a_{ij}[/latex] is the abundance of species j in sample unit i
• [latex]a_{hj}[/latex] is the abundance of species j in sample unit h
• [latex]a_{i\cdot}[/latex] is the total abundance of all species in sample unit i
• [latex]a_{h\cdot}[/latex] is the total abundance of all species in sample unit h

This is the same formula we saw in the section about distance measures.  For our purposes here, note the summations:

• In the numerator, a difference is calculated for each species and then those differences are summed together
• In the denominator, the total abundance is summed for each sample unit and then those abundances are summed together.

Clarke (1993) observed that this formula means that each species contributes uniquely to the dissimilarity between two sample units.  In other words, we can consider how much of the total dissimilarity between two sample units is due to each species.

When there are multiple sample units, there are also multiple dissimilarities (i.e., pairwise combinations) to consider – each species can contribute to the dissimilarity between each pair of sample units.  If our purpose is to quantify the contribution of each species to the differences between two groups, we have to consider all of these dissimilarities.

The average dissimilarity for each pairwise combination can be calculated directly via the vegan::meandist() function:

meandist(dist = vegdist(Oak1),
grouping = Oak_explan$Grazing)

          Always     Never      Past
Always 0.6876976 0.7262910 0.6730906
Never  0.7262910 0.6872665 0.6924324
Past   0.6730906 0.6924324 0.6935371
attr(,"class")
[1] "meandist" "matrix"  
attr(,"n")
grouping
Always  Never   Past 
    17     24      6 

The distances shown here are a symmetric square matrix where each value is the average distance between two sample units.  Values on the diagonal are the average distances between observations in the same group; all other values are the average distances between an observation in one group and an observation in another group.  For example, the largest average distance here, 0.726, is between the ‘Always’ and ‘Never’ groups.

Similarity percentage (SIMPER) partitions the Bray-Curtis dissimilarity as described above for every pair of sample units, and then calculates the average contribution of each species to the difference between the sample units.  These contributions are relativized so that the average contributions of all species sum to 1.  Statistical significance of these contributions is assessed by permuting the group identities.

Note that the title is misleading: a high value for SIMPER means that a species has a high contribution to the difference between the two groups, not that it has high similarity between them.

Published SIMPER Examples

Encarnação et al. (2015) compared subtidal soft-bottom macrofaunal assemblages in areas influenced or not influenced by submarine groundwater discharge.

Evangelista et al. (2016) compared vegetation data from 1972 and 2014, and used SIMPER to identify species that exhibited strong temporal changes.

da Costa et al. (2018) used SIMPER and PCA to examine plant growth promoting bacteria.  In particular they calculated the SIMPER value for each treatment-control pair and used this value as an index of invasion.

Gibert & Escarguel (2019) consider ways that SIMPER patterns can indicate whether community assembly is dominated by niche- or dispersal-related processes.

SIMPER in R (vegan::simper())

SIMPER is available in the vegan package.  Its usage is:

simper(comm,
group,
permutations = 999,
parallel = 1,
...
)

The arguments include:

• comm – a compositional data object. Required.
• group – a grouping variable.  Usually included.  If excluded, this function returns the average contribution of each species to the average pairwise dissimilarity in the dataset.
• permutations – number of permutations to perform when testing if the average contribution of that species when the group identities are randomly permuted.

The output of this function is a list (collection of dataframes).  Each dataframe pertains to a different pairwise combination of groups (e.g., levelA vs. levelB) and is named following the format ‘levelA_levelB’.  Notes about the output in each dataframe:

• Species are in descending order – the species that contributes the most is listed first.
• Column descriptions:
  • average = average contribution of this species to the average dissimilarity between observations from the two groups.  The sum of this column is the average dissimilarity between observations from the two groups.
  • sd = standard deviation of the contribution of this species (i.e., based on its contribution to all dissimilarities between observations from the two groups).
  • ratio = ratio of average to sd.  Basically, a coefficient of variation (CV).
  • ava, avb = average abundance of this species in each of the two groups.  Only included if a grouping variable (group) was included in the original call to simper().
  • cumsum = cumulative contribution of this and all previous species in list.  Based on average, but expressed as a proportion of the average dissimilarity.  As a result, the maximum value of this column is 1.
  • p = permutation-based p-value; probability of getting a larger or equal average contribution for each species if the grouping factor was randomly permuted.

Oak Example

Applying SIMPER to our data:

simper.Grazing <- simper(Oak1, Oak_explan$Grazing)

In our example, there are three levels and thus three pairwise combinations (i.e., n(n-1)/2).  We can extract information separately for each pairwise combination by indexing the relevant dataframe within the list.  For example:

summary(simper.Grazing)$Always_Past %>%
round(3) %>%
head()

       average    sd ratio   ava   avb cumsum     p
Frvi     0.023 0.022 1.059 0.588 0.400  0.034 0.748
Trla     0.022 0.023 0.938 0.471 0.333  0.067 0.330
Mebu     0.020 0.022 0.905 0.376 0.333  0.096 0.285
Acmi     0.019 0.020 0.956 0.412 0.233  0.125 0.070
Rhdi.s   0.014 0.010 1.373 0.358 0.533  0.146 0.078
Nepa     0.014 0.020 0.677 0.235 0.167  0.166 0.224

For example, ‘Frvi’ is the species that contributes the largest amount of the difference between these two groups.  The cumulative contribution of ‘Frvi’ (cumsum) is it’s average contribution (i.e., average) divided by the overall average dissimilarity between these two groups (calculated above):

0.023 / 0.673 = 0.034.

We can also re-organize these results into a single dataframe.  While doing so here, I’ll also keep track of the order of the species within each comparison.

comparisons <- c("Always_Past", "Always_Never", "Past_Never")

simper.results <- c()

for(i in 1:length(comparisons)) {
require(tidyverse)
temp <- summary(simper.Grazing)[as.character(comparisons[i])] %>%
as.data.frame()
colnames(temp) <- gsub(
paste(comparisons[i],".", sep = ""), "", colnames(temp))
temp <- temp %>%
mutate(Comparison = comparisons[i],
Position = row_number()) %>%
  rownames_to_column(var = "Species")
simper.results <- rbind(simper.results, temp)
}

  Species    average         sd     ratio       ava       avb     cumsum
1    Frvi 0.02285920 0.02158049 1.0592528 0.5882353 0.4000000 0.03396154
2    Trla 0.02198060 0.02342799 0.9382194 0.4705882 0.3333333 0.06661777
3    Mebu 0.02008343 0.02220031 0.9046462 0.3764706 0.3333333 0.09645539
4    Acmi 0.01903871 0.01992442 0.9555464 0.4117647 0.2333333 0.12474090
5  Rhdi.s 0.01435717 0.01045780 1.3728664 0.3584131 0.5329457 0.14607111
6    Nepa 0.01360838 0.02011243 0.6766152 0.2352941 0.1666667 0.16628886
      p  Comparison Position
1 0.721 Always_Past        1
2 0.356 Always_Past        2
3 0.283 Always_Past        3
4 0.096 Always_Past        4
5 0.069 Always_Past        5
6 0.218 Always_Past        6

Our dataset includes 103 species and there are 3 pairwise comparisons of grazing treatments, so the simper.results object has 309 rows.

Having the data in this format permits easy indexing and summarizing of information as illustrated below.

Using SIMPER Results

Focus on Individual Species

We can use the SIMPER results to compare responses across pairwise combinations.  For example, we could focus on an individual species and compare it’s importance for different pairwise comparisons:

simper.results %>%
filter(Species == "Frvi")

  Species    average         sd     ratio       ava       avb     cumsum
1    Frvi 0.02285920 0.02158049 1.0592528 0.5882353 0.4000000 0.03396154
2    Frvi 0.02484323 0.02468804 1.0062858 0.5882353 0.3333333 0.03420561
3    Frvi 0.02423108 0.02526568 0.9590513 0.4000000 0.3333333 0.07028970
      p   Comparison Position
1 0.721  Always_Past        1
2 0.260 Always_Never        1
3 0.511   Past_Never        2

‘Frvi’ is one of the species that contributes most to the differences between sample units from different groups, though it is not statistically significant (probably because of its high variability among sample units).

We can also filter the results to focus on those that are statistically significant:

simper.results %>%
filter(p <= 0.05) %>%
select(Species, average, Comparison, Position)

   Species     average   Comparison Position
1     Aqfo 0.013522186  Always_Past        8
2     Trla 0.023175569 Always_Never        2
3   Syal.s 0.021775672 Always_Never        3
4     Acmi 0.017852658 Always_Never        5
5   Roeg.s 0.009986365 Always_Never       13
6     Plla 0.007682389 Always_Never       36
7     Adbi 0.007646766 Always_Never       37
8     Taof 0.007643184 Always_Never       38
9     Lope 0.007363360 Always_Never       40
10    Popr 0.006859677 Always_Never       43
11  Quga.s 0.006552076 Always_Never       48
12    Kocr 0.006200026 Always_Never       50
13    Daca 0.005903157 Always_Never       53
14    Erla 0.004826316 Always_Never       69
15    Elgl 0.004818007 Always_Never       71
16    Feru 0.004744426 Always_Never       73
17    Agte 0.004352958 Always_Never       80
18  Arme.s 0.004247614 Always_Never       82
19    Pogr 0.003994785 Always_Never       86
20  Syal.s 0.024439782   Past_Never        1
21  Rhdi.s 0.016881490   Past_Never        6
22    Aqfo 0.016242687   Past_Never        7
23    Sado 0.014907039   Past_Never        9
24    Frbr 0.009676594   Past_Never       20
25  Pyfu.s 0.009057556   Past_Never       28

Many more species have significant values in the Always_Never combination (18) than in the Always_Past combination (1) or the Past_Never combination (6) – an indication that differences are strongest between these two groups?

A few species are identified as important in multiple comparisons.  For example, ‘Aqfo’ is significant in the Always_Past and ‘Past_Never’ comparisons – this may be an indication that its abundance patterns are different in the ‘Past’ group than in the ‘Always’ or ‘Never’ groups.  However, SIMPER doesn’t indicate which group a species was more strongly associated with; see Indicator Species Analysis for that.

What do you think about the distribution patterns of ‘Syal.s’?

Statistical significance in SIMPER is very sensitive to abundance patterns – see ‘Conclusions’ below.

Adding up the contributions of all species in each pairwise combination:

simper.results %>%
group_by(Comparison) %>%
summarize(sum.average = sum(average))

# A tibble: 3 × 2
  Comparison   sum.average
  <chr>              <dbl>
1 Always_Never       0.726
2 Always_Past        0.673
3 Past_Never         0.692

Compare to the results from meandist() above and verify that these totals are the same.

Examine Patterns Across Species

Another way to use these data would be to consider whether the differences are ‘driven’ by a subset of the species or reflect small contributions from lots of species.  Gibert & Escarguel (2019) propose that this can be used to determine whether species distributions are driven by niche- or dispersal-assembly processes.

For example, the cumulative and average contributions could be graphed and compared against pairs of groups:

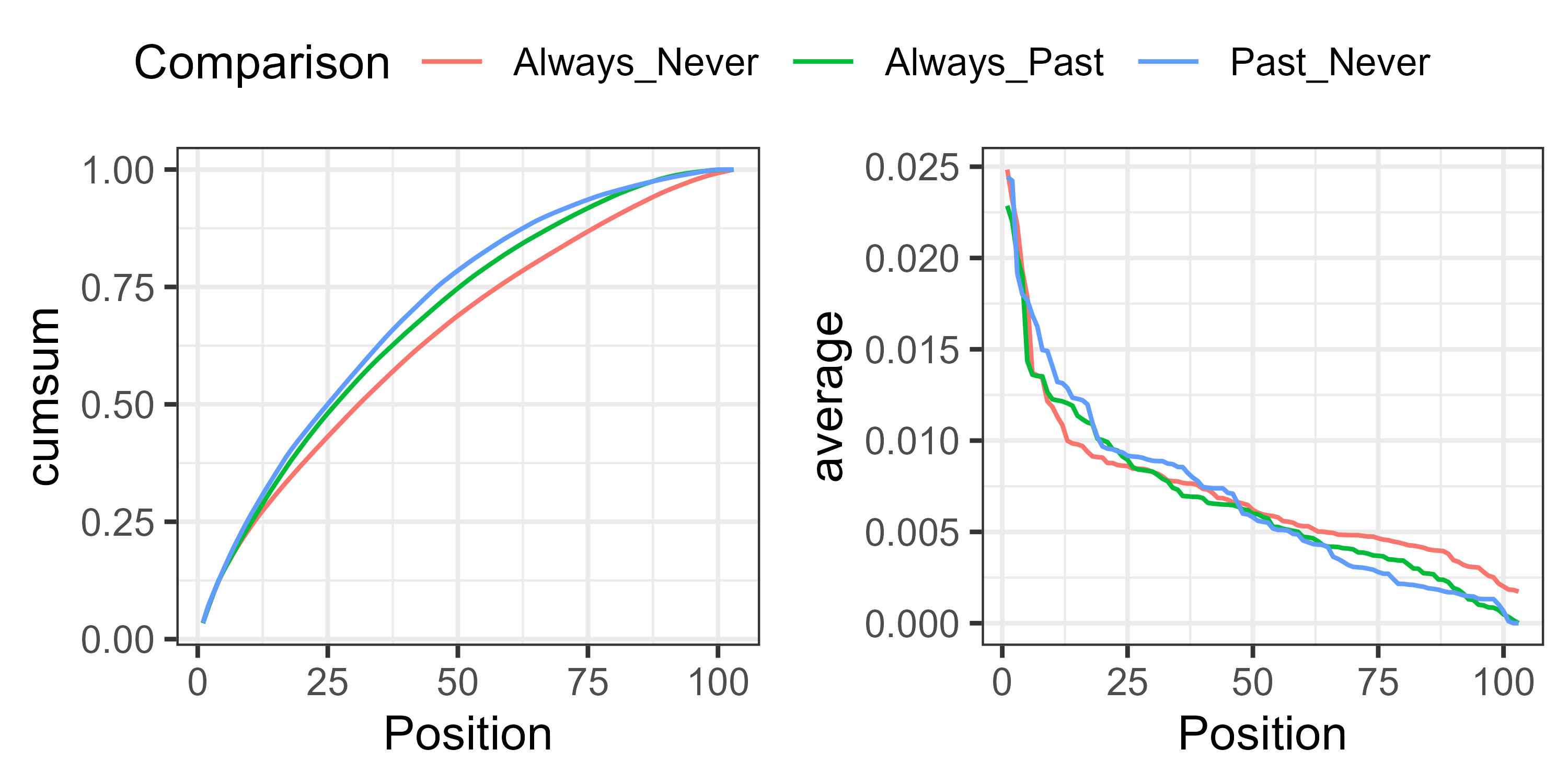
In this case, the cumulative contribution of species is more even for the Always_Never comparison than for the others (left), and every species contributes some non-zero amount to the compositional difference (right).

Code to create the above graphic follows:

p1 <- ggplot(data = simper.results,
aes(x = Position, y = cumsum)) +
geom_line(aes(colour = Comparison)) +
theme_bw()

p2 <- ggplot(data = simper.results,
aes(x = Position, y = average)) +
geom_line(aes(colour = Comparison)) +
theme_bw()

library(ggpubr)

ggarrange(p1, p2, common.legend = TRUE)

ggsave("graphics/simper.Grazing.png", width = 5, height = 2.5,
units = "in", dpi = 600)

Conclusions

The help files (?simper) provide some caveats for the interpretation of SIMPER.  For example:

“The method gives the contribution of each species to overall dissimilarities, but these are caused by variation in species abundances, and only partly by differences among groups. Even if you make groups that are copies of each other, the method will single out species with high contribution, but these are not contributions to non-existing between-group differences but to random noise variation in species abundances.”

In general, this approach doesn’t appear to have received much attention from ecologists – perhaps because of these concerns about how to interpret the results – though the work of Gibert & Escarguel (2019) suggests that other ways to use this information could be developed.  For example, comparing patterns within groups to patterns between groups might be a fruitful way forward…

Each pair of groups is considered separately in SIMPER, whereas Indicator Species Analysis allows you to compare multiple groups to one another.  

References

Clarke, K.R. 1993. Non-parametric multivariate analyses of changes in community structure. Australian Journal of Ecology 18:117-143.

da Costa, P.B., S.B. de Campos, A. Albersmeier, P. Dirksen, A.L.P. Dresseno, O.J.A.P. dos Santos, K.M.L. Milani, R.M. Etto, A.G. Battistus, A.C.P.R. da Costa, A.L.M. de Oliveira, C.W. Galvão, V.F. Guimarães, A. Sczyrba, V.F. Wendisch, and L.M.P. Passaglia. 2018. Invasion ecology applied to inoculation of plant growth promoting bacteria through a novel SIMPER-PCA approach. Plant and Soil 422:467-478.

Encarnação, J., F. Leitão, P. Range, D. Piló, M.A. Chícharo, and L. Chícharo. 2015. Local and temporal variations in near-shore macrobenthic communities associated with submarine groundwater discharges. Marine Ecology 36(4):926-941.

Evangelista, A., L. Frate, M.L. Carranza, F. Attore, G. Pelino, and A. Stanisci. 2016. Changes in composition, ecology and structure of high-mountain vegetation: a re-visitation study over 42 years. AoB Plants 8:plw004.

Gibert, C., and G. Escarguel. 2019. PER-SIMPER—A new tool for inferring community assembly processes from taxon occurrences. Global Ecology and Biogeography 28(3):374-385.