A – Math and Science During Play

One way that children learn about the world is by exploring and experimenting during play. Exploration and hands-on learning naturally involves many cognitive skills.

In fact, one study found that during unstructured free play, 4- to 6-year-old children spent about half of their time engaged in some form of math or science-related activities. This was true regardless of gender or ethnicity.

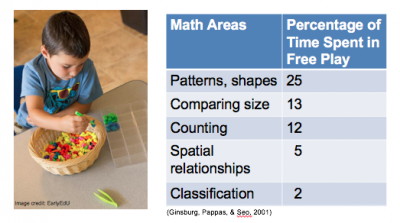
Looking at the time spent on math and science activities, children spent about:

• 25 percent examining pattern and shapes
• 13 percent comparing sizes and amounts
• 12 percent counting
• 5 percent on spatial relations, such as the position, direction, or distance of objects relative to each other
• 2 percent on classification

These activities are all part of the Mathematics Development domain, and they demonstrate how much math is a part of children’s (and adults’) daily lives.

Children’s play involved math, language, and thinking, even though math was not the primary focus of their play.

Children talked about things like “How much is a lot?” and “How little is little?” They often used their bodies to show size. They might, for instance, stretch their arms wide to show how big a pumpkin is or hold fingers close together to show that something was a little bit scary.

B – Counting and Cardinality

First Mathematics Development Subdomain

One of the four Mathematics Development subdomains is Counting and Cardinality.

As we covered in the previous lesson on early cognitive development, prior to 3 years of age, children have already begun to develop their skills in numbers, quantity comparison, spatial awareness, and sorting. From 3 to 5 years old, children use those foundational skills to build understanding about relations, patterns, and combinations of numbers.

The Counting and Cardinality subdomain encompasses many skills.

Counting includes:

• Knowing the names of numbers and how to write the numbers themselves
• Knowing the counting sequence and understanding the one-to-one object-number correspondence

Cardinality is understanding that the last number word of an array of counted items has a special meaning. It represents the set as a whole and the quantity of this set of items. This includes:

• Understanding the relationship between number and quantity
• Being able to recognize the number of a small set of objects without counting
• Making number comparisons

Performance on Cardinality Tasks

Between ages 3 and 5, children develop significant skills in mathematics.

But how do children get from small-number recognition and large-quantity comparisons to writing, counting, and understanding the number-quantity relationship, sometimes called cardinality?

Scientists studied this by asking 2-and-a-half- to 3-and-a-half-year-old children to give a puppet a specific number of toy dinosaurs.

Interactive: Cardinal Tasks

This is an interactive! Use the slider to explore the graph.

Interestingly, all children were also tested for their ability to count, and all children could accurately count up to four or five objects. So even though these children could count to four or five, they had not figured out the relationship between counting numbers and measuring quantities, what is called the concept of cardinality.

Scientists think that children develop the concept of cardinality for one object first, then two objects, then three objects. Then they expand this to any number of objects.

Understanding Cardinality

In a separate task, the children from this study were also asked to help a puppet find out how many toys they had. This is different from simply counting toys because children have to understand the concept of cardinality–that the last number in a counting sequence is also the number for the quantity of objects just counted—to answer the question: “How many?”

What scientists found was that the children who grabbed in the dinosaur toy task did not understand this concept.

However, there were a few children who had not grabbed in the dinosaur task and had instead, counted the toy dinosaurs before giving them to the puppet. All these children were 3-and-a-half-year-olds. The children who had counted understood the concept of cardinality.

What this means is that when children figure out the concept of cardinality, they begin to apply it in their daily lives when asked for a specific number of objects or when asked to figure out how many objects they have.

It also suggests that children don’t begin to understand the concept of cardinality until around 3-and-a-half years of age.

Vroom Tip

Check out this Vroom tip to get more ideas about how to help build children’s cognitive development in the area of reasoning and problem-solving skills.

Does this tip make sense in the context of an early learning environment? And if not, how might you adapt the activity to better fit that environment?

C – Operations and Algebraic Thinking

Second Mathematics Development Subdomain

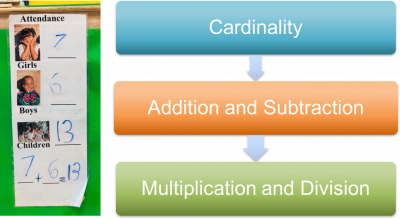
The second Mathematics Development subdomain is Operations and Algebraic Thinking.

This includes the development of reasoning about patterns and arithmetic skills, such as being able to solve the mathematical operations of addition and subtraction.

It is widely understood that the development of arithmetic skills starts about the age of 3 and that it correlates with children’s understanding of cardinality.

In addition, children’s development of arithmetic skills follows this pattern:

• Cardinality develops.
• Addition leads to an understanding of subtraction.
• Knowledge of addition and subtraction aids in the understanding of multiplication. (For example, 2 x 3 means adding 2 to itself three times).
• Understanding multiplication contributes to knowledge of division.

Video: Let’s Talk About Math: Everyday Fun with Addition and Subtraction: (3:00)

This video, Let’s Talk About Math: Everyday Fun with Addition and Subtraction, shows children, birth to age 5, engaged in math-related activities that illustrate math development. This video is 3-minutes long.

Note that this video includes infants and toddlers and overlaps with content from the previous session.

While viewing the video, think about the following questions:

• How do young children develop math skills, particularly those related to addition and subtraction?
• How can adults foster these skills?

Understanding Quantity

Researchers have found that learning arithmetic (addition and subtraction) and children’s understanding of quantity is so connected that improving children’s understanding of quantity can help them learn arithmetic later.

Scientists showed this by designing a simplified version of the board game Chutes and Ladders to improve preschool children’s understanding of cardinality.

In the experimental board game (called The Great Race), 4- and 5-year-old children spun a spinner with a 1 and a 2 on it. If the spinner landed on the 1, children advanced one space. If it landed on the 2, they advanced two spaces. The experimenter played this game with children one-on-one for four 15- to 20-minute sessions during a 2-week period.

Children were tested for various arithmetic skills, including magnitude comparison, comparing which of two numbers is larger or smaller, and addition problems.

Magnitude comparison was measured by asking children to compare two numbers on a page—for example, 1 on the left versus 6 on the right. The experimenter asked the children, “Jane has one cookie, Sarah has six. Which one is more—one cookie or six cookies?”

Children were also tested with some simple addition problems, such as 2 + 1 and 2 + 3.

Scientists found that children who played the number board game performed better on the arithmetic skills tests than children who played a similar game based on colors or who had participated in other number learning activities, such as object-counting tasks.

Social Benefits

Some may find it surprising that improving children’s understanding of cardinality can also benefit them socially. Understanding cardinality and mathematical skills, in general, has been found to be related to children’s ability to share.

For example, 3- to 5-year-old children were asked to share blocks equally between two dolls. The trick was that there were single, double, and triple blocks, but the goal was for the child to make sure that both dolls had the same total number of blocks.

If the child gave a double block to one recipient, they would have to give two single blocks to the other to ensure that they had equal amounts.

Four-year-olds struggled greatly with this task, often treating the double blocks as if they were equivalent to the single blocks, even when they were able to count the total number of blocks accurately.

In contrast, 5-year-olds were much more successful on this task.

Reasoning about Patterns

Reasoning about patterns is also an important part of the subdomain Operations and Algebraic thinking.

The development of pattern-creation and pattern-completion skills is a sign of children’s growing ability to think more abstractly and flexibly about the world around them.

Before 5 years of age, children develop simple rules for completing patterns, such as: Match the color of the fifth item.

They struggle with patterns that require noting the relationships between multiple items, such as triangle first, then circle, then square.

Also, after sorting objects based on one attribute, such as color, 3- to 4-year-olds have a difficult time re-sorting the same objects based on a different attribute, such as size.

Practicing these kinds of games in the early learning setting or at home will help children build their abstract reasoning skills.

D – Measurement

Third Mathematics Development Subdomain

The third Mathematics Development subdomain is Measurement.

Measurement may seem like a fairly basic skill, but it requires some fairly sophisticated understanding.

It requires the measurer to realize that a measurement is only useful if it is done using a single unit of measure.

For example, measuring the height of a block tower with a teddy bear, two blocks, and a ball is not very useful. But measuring the height with four matching balls is much more useful for replicating the measurement and making comparisons.

Measuring also requires the knowledge that if you want to compare the measurements of two objects, you should use the same measures for each.

For example, if you want to compare the height of your block tower to the height of your friend’s block tower, measuring one in number of teddy bears and the other in number of blocks will make the comparison difficult.

Measuring Continuous Substances

In particular, children have difficulty with what scientists call continuous substances. Continuous substances don’t have automatic units of measure that are easy to identify or count. For example, sand is a continuous substance. You can put it in cups and count the number of cups or weigh it on a scale, but it’s not like counting blocks.

Scientists have shown that the ability to measure continuous substances develops between the ages of 3 and 5 years.

Scientists demonstrated this by presenting preschool children with one box with three cups containing 3 ounces of sand each and another box with two cups containing 3 ounces of sand each.

They would then ask the children to identify the larger quantity in two different comparisons, using these questions:

• Which box had more cups?
• Which box had more sand?

Younger preschool children had a hard time with the more sand comparison; they got it wrong more often than they got the cups comparison wrong. Older preschool children were able to do both comparisons.

This suggests that younger children were disregarding the use of the cups as a unit of measure for the sand.

Giving young children practice with units of continuous substances and guiding them through the quantity comparisons can help them develop quantity comparison skills with continuous substances.

E – Geometry and Spatial Sense

Fourth Mathematical Development Subdomain

The subdomain of Geometry and Spatial Sense includes the ability to recognize, build, and sort shapes.

From 3 to 5 years of age, children develop the skills necessary to recognize atypical examples of shapes. The development of these skills varies considerably between children and usually occurs first for shapes that retain their appearance despite changes in their size and orientation.

Many parents and some educators begin shape instruction in early infancy with board books and other materials. Children begin to identify shapes at a fairly young age as well. However, geometry and spatial reasoning of this kind is more than standard shape recognition.

Younger children base many of their shape judgments on visual characteristics, rather than the geometric properties. Often, children rely on a shape’s orientation in the space. Also, children will often recognize standard shapes but not atypical ones, such as the triangle circled in red on this slide; children’s ability to recognize atypical shapes as part of a specific shape category varies from shape to shape.

Scientists have found that shapes that retain their general shape (e.g., circles or rectangles) despite their size or orientation are easier for children to learn accurately, regardless of the complexity of their geometric properties.

Shapes like triangles can be much more difficult to recognize when they are not in their standard form.

Interactive: Social Support

This is an interactive! Use the slider to explore the graph.

References

Bennet, J., & Muller, U. (2010). The development of flexibility and abstraction in preschool children. Merrill-Palmer Quarterly, 56(4), 455-473.

Bradley, M. (1943). Chutes and ladders [Board game].

Fisher, K., Hirsh-Pasek, K., Newcombe, N., & Golinkoff, R. (2013). Taking shape: Supporting preschoolers’ acquisition of geometric knowledge through guided play. Child Development, 84(6), 1872-1878.

Fydman, O., & Bryant, P. (1988). Sharing and the understanding of number equivalence by young children. Cognitive Development, 3(4), 323-339.

Ginsburg, H. P., Pappas, S., & Seo, K.-H. (2001). Everyday mathematical knowledge: Asking young children what is developmentally appropriate. In S. L. Golbeck (Ed.), The Rutgers Invitational Symposium on Education Series. Psychological Perspectives on Early Childhood Education: Reframing Dilemmas in Research and Practice. (pp. 181-219). Lawrence Erlbaum Associates Publishers.

Huntley-Fenner, G. (2001). Why count stuff? Young preschoolers do not use number for measurement in continuous dimensions. Developmental Science, 4(4), 456-462.

Ramani, G., & Siegler, R. (2008). Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Development, 79(2), 375-394.

Satlow, E., & Newcombe, N. (1998). When is a triangle not a triangle? Young children’s developing concepts of geometric shape. Cognitive Development, 13(4), 547-559.

Siegler, R. & Braithwaite, D. (2017). Numerical development. Annual Review of Psychology, 68, 187-213.

Siegler, R., & Ramani, G. (2009). Playing linear number board games—but not circular ones—improves low-income preschoolers’ numerical understanding. Journal of Educational Psychology, 101(3), 545-560.

U.S. Department of Health and Human Services, Administration for Children and Families, Office of Head Start. (n.d.) Interactive Head Start Early Learning Outcomes Framework: Ages birth to five. [Website]

Vroom. (n.d). Vroom tips. [PDF]

Wynn, K. (1990). Children’s understanding of counting. Cognition, 36(2), 155-193.

Zero to Three. (2016). Let’s talk about math: Everyday fun with addition and subtraction. [Video]