8 Water Burns: Moisture and Latent Heat

Water is such a remarkable molecule for the Earth’s climate. We’ve already talked about

• Water vapor, and its role as the strongest heat-trapping gas,
• Ice and snow, and their impact on surface albedo, and
• Cloud water and ice, and their effect on both shortwave and longwave radiation.

Later we’ll dive into the role of the ocean in storing energy and transporting heat, as well as ice sheet effects on sea level rise.

The next topic, though, is much less well known, but fundamental to so many aspects of Earth’s climate and how it changes. We’ll discuss the effect of latent heating, the energy that’s released when a change of phase occurs. These include:

• The cooling associated with evaporation,
• The energy released by condensation,
• Energy required to melt ice,
• And energy released in the freezing process.

The energy exchanged in these processes is called latent heat because it occurs without a temperature change. When a quantity of water evaporates, latent heat is extracted, resulting in cooling. Although it might move over large distances before it turns back into liquid, all of that hidden latent heat is released upon condensation.

Latent heat exchange from the condensation/evaporation of water is huge! The latent heat of vaporization of water is L_v = 2.5e6 J/kg, while the specific heat of water is C = 4.2e3 J/kg/K. The latter number is large among common materials: it takes a lot of energy to change the temperature of water. But the latent heat is massive, so evaporating 1 kg of water requires the same amount of energy as changing almost 600 kg of water by 1^o C.

The latent heat of fusion of water L_f = 3.4e5 J/kg is not as large, but still ends up being about 80 times the energy needed to raise water by 1^o C.

Inuit musician Tanya Tagaq‘s song “Cold” is certainly the most remarkable piece of art that references the ratio between L_f and C, and is indeed one of the most stunning climate justice anthems.

Preliminaries

More water vapor can exist in air at higher temperatures, exponentially increasing with temperature (almost). There are a few different ways to measure water vapor concentrations, and in this text we’ll use the specific humidity, which is the mass of water vapor divided by the mass of moist air. Assuming the partial pressure of water vapor is small compared to that of air, the saturation specific humidity q_s can be written as

[latex]q_s = q_{s0}\ {p_0 \over p} exp(- {L_v \over R_v} (T^{-1} - T_0^{-1}))[/latex]

where q_s0 = 3.8 g/kg is the saturation specific humidity at T₀ = 0^o C and p₀ = 1000 hPa, p is the pressure, L_v is the latent heat of vaporization defined above, R_v = 461.5 J/kg/K is the gas constant for water vapor. This function is close to an exponential increase with temperature, with growth rate around 7 %/^oC. There is an approximately factor of 10 difference between the saturation specific humidity at 0^o C and at 35^o C.

The saturation specific humidity is the maximum amount of water that can exist in air before saturation occurs. The specific humidity q, which we’ll also refer to as the humidity content or the moisture content, is constrained to remain below the saturation specific humidity, with the exception of occasional supersaturations. Relative humidity R is the ratio between the actual specific humidity q and the saturation value,

[latex]R = q/q_s[/latex].

When humid air cools, the saturation specific humidity decreases while the specific humidity stays the same, so eventually R reaches 100% and condensation occurs. In the atmosphere, the cooling usually comes from rising motion, so most precipitation occurs when humid air rises. Learn more about the processes involved in condensation by watching the video below.

When condensation occurs, latent heat is released, which warms the air. It’s often useful to consider the specific humidity of water vapor in units of temperature, L_vq/c_p, with c_p = 1006 J/kg/K the specific heat at constant pressure of air. This is the temperature that air would warm up by if all its moisture were condensed out.

The plot below shows the climatology of surface water vapor in units of temperature. The values are huge! Annual mean water vapor concentration averages around 45 K in warm tropical oceans. Midlatitude values are large too, and only in very cold regions does the value go lower than 5 K. All of this latent energy in near-surface air does end up warming up air, within phenomena like tropical cyclones, overturning circulations, or midlatitude cyclones, usually within a couple weeks timescale.

Surface humidity content, measured in kelvin (i.e., multiplied by L_v/c_p = 2.5 K/(g/kg)). Source: Durran and Frierson, 2013. 

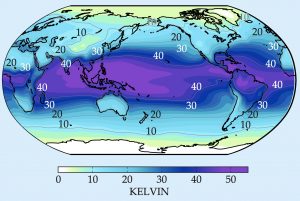
The saturation specific humidity provides an upper limit on humidity content, meaning that the highest humidity values are confined to the warmest parts of the atmosphere. Since temperatures decrease with elevation in the troposphere, most of the water vapor is also confined to the lower atmosphere.

While cold air must be dry, because saturation specific humidity is small, warmer air need not necessarily be dry, if the relative humidity is low. This occurs in places like deserts, and depends on features like the local rainfall, rivers, and vegetation.

Surface humidity content, measured in kelvin (i.e., multiplied by L_v/c_p = 2.5 K/(g/kg)), in January and July. 

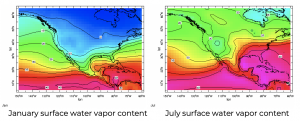
Still, temperature provides a strong constraint on surface humidity, even over land. Across the North America, summer humidities are much larger than those in winter, often by a factor of two or three. Even in Seattle, where it rains so much in the winter, and so seldom in the summer, humidities are higher in the summer.

Water vapor and global warming

All of the above is suggestive of a tendency of humidity around the world to increase as temperatures rise. Indeed, humidities have been rising, and are expected to continue, approximately at a rate of 7%/K, as it would if relative humidities remain constant.

The relative humidity is determined by the cycle of water through the atmosphere. Evaporation occurs from warm oceans, lakes, or transpiration from plants. Each of these are proportional to 1-R; a drier atmosphere evaporates more. As they move around within the atmosphere, air parcels carry with them a humidity amount determined by the temperature of last saturation. Evaporation and condensation balance in a steady state, and the locations and frequencies of these determine the relative humidity of the atmosphere.

Water vapor is the strongest heat-trapping gas, so as humidity rises in a warmer climate, the greenhouse effect also increases. This leads to an amplification of warming, in a positive feedback cycle.

As water vapor increases with temperature, so do hydrologic cycle extremes. Extreme rainfall is increasing across the globe, and is without a doubt one of the most important consequences of fossil fuel burning. Drought also increases as temperatures increase. Land surfaces that are away from rainy weather are dried out more rapidly by the increased water vapor holding capacity.

We’ll detail all these aspects of water vapor in future chapters, but first we need to study the impacts of condensation. A surprising amount of climate impacts depend on the latent heat release from higher humidity levels, from rising weather systems and warming aloft, to interconnections between polar regions and the rest of the planet. Since the strength of condensation as a heat source is not very well-appreciated, let’s discuss an everyday occurrence.

Condensation and Cold Drinks

Everyone knows evaporation cools you. It’s why sweating cools us down. Swamp coolers, the systems in the desert that spray out mists of water, give out rushes of cold air when the droplets evaporate.

Few people, however, recognize the strength of the opposite process, condensation as a heat source. Dale Durran and I developed an experiment to show the every day importance of condensation. We show that condensation affects how quickly cold drinks warm up in humid climates.

I remember from growing up near the ocean in North Carolina how quickly cold drinks become drenched in condensation during the summer, and the ice in a drink melting especially quickly. These phenomena are not unrelated. Since the glass is cold, air around it has a low saturation humidity. Condensation occurs, forming droplets on the glass. But there is also heat released, which ends up making a significant impact on warming the drink, and melting the ice in it.

To test the importance of this process, we used an old mothballed atmospheric chamber, and put in cold drink cans for 5 minutes at a time. Afterwards we measured the temperature and the amount of condensation on the can.

Left: then undergraduate research Stella Choi measuring a can that was just removed from the environmental chamber (background). Right: weighing the condensation that formed on the can surface.

Our results showed that under conditions similar to the Gulf South, cans would heat up twice as quickly due to the condensation, as compared to a hot desert climate like Phoenix.

How about the most humid conditions on Earth? Dharan, Saudi Arabia hit a world record humidity of 37 g/kg in 2003, on a day when the winds were blowing in from the Persian Gulf. Under those conditions, we predict a 12-ounce drink in the shade would heat up from 0^o C to 14^o C (57^o F) within just five minutes. Over 8^o C comes from condensation. In a dry environment, the can would only warm by 6^o C.

Next time you see drips on your drink, think of the power of condensation — and get a koozy! It’s an effective way to keep condensation off of a can, while providing insulation as well.

Latent Heat and Climate

The surface of the Earth cools significantly by evaporation and sublimation (ice turning directly into water vapor), ultimately transferring this heat to the atmosphere when rain and snow occur. How does this compare to other methods of energy transfer between the surface and atmosphere? Plotted below is the Earth’s energy budget, including shortwave and longwave radiation, as well as latent and thermal heat fluxes.

Earth’s energy budget. Source: NASA.

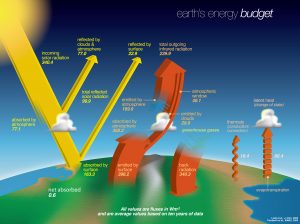
Let’s consider terms that transfer energy from the atmosphere to the ocean, and vice versa. Latent heating transfers an average of 86.4 W/m² from the surface to the atmosphere in the global mean. Thermals, the conduction and convection of heat directly from the surface to atmosphere, amounts to 18.4 W/m² in the global mean. The net longwave radiative transfer from surface to atmosphere involves a few different terms. Longwave radiation is emitted directly from the surface at an average of 398.2 W/m², but 40.1 W/m² makes it straight to space, so the heating of the atmosphere by the surface via longwave radiation is 358.1 W/m². The longwave heating of the surface by the atmosphere, the back radiation, is 340.3 W/m². Therefore the net longwave radiative transfer is only 17.8 W/m². Comparing these three terms (latent heating, thermals, and net longwave from atmosphere to ocean) shows that latent heating makes up over 70% of the transfer of energy from surface to atmosphere.