Student Learning Outcomes

By the end of this chapter, the student should be able to:

• Be able to identify and develop the null and alternative hypothesis
• Identify the consequences of Type I and Type II error.
• Be able to perform an one-tailed and two-tailed hypothesis test using the critical value method
• Be able to perform a hypothesis test using the p-value method
• Be able to write conclusions based on hypothesis tests.

Introduction

As an example, in Microeconomics the theory of consumer choice begins with certain assumption concerning human behavior. From these assumptions a theory of how consumers make choices using indifference curves and the budget line. This theory gave rise to a very important prediction, namely, that there was an inverse relationship between price and quantity demanded. This relationship was known as the demand curve. The negative slope of the demand curve is really just a prediction, or a hypothesis, that can be tested with statistical tools.

Unless hundreds and hundreds of statistical tests of this hypothesis had not confirmed this relationship, the so-called Law of Demand would have been discarded years ago. This is the role of statistics, to test the hypotheses of various theories to determine if they should be admitted into the accepted body of knowledge; how we understand our world. Once admitted, however, they may be later discarded if new theories come along that make better predictions.

Not long ago two scientists claimed that they could get more energy out of a process than was put in. This caused a tremendous stir for obvious reasons. They were on the cover of Time and were offered extravagant sums to bring their research work to private industry and any number of universities. It was not long until their work was subjected to the rigorous tests of the scientific method and found to be a failure. No other lab could replicate their findings. Consequently they have sunk into obscurity and their theory discarded. It may surface again when someone can pass the tests of the hypotheses required by the scientific method, but until then it is just a curiosity. Many pure frauds have been attempted over time, but most have been found out by applying the process of the scientific method.

This discussion is meant to show just where in this process statistics falls. Statistics and statisticians are not necessarily in the business of developing theories, but in the business of testing others’ theories. Hypotheses come from these theories based upon an explicit set of assumptions and sound logic. The hypothesis comes first, before any data are gathered. Data do not create hypotheses; they are used to test them. If we bear this in mind as we study this section the process of forming and testing hypotheses will make more sense.

One job of a statistician is to make statistical inferences about populations based on samples taken from the population. Confidence intervals are one way to estimate a population parameter. Another way to make a statistical inference is to make a decision about the value of a specific parameter. For instance, a car dealer advertises that its new small truck gets 35 miles per gallon, on average. A tutoring service claims that its method of tutoring helps 90% of its students get an A or a B. A company says that women managers in their company earn an average of $60,000 per year.

A statistician will make a decision about these claims. This process is called ” hypothesis testing.” A hypothesis test involves collecting data from a sample and evaluating the data. Then, the statistician makes a decision as to whether or not there is sufficient evidence, based upon analyses of the data, to reject the null hypothesis.

In this chapter, you will conduct hypothesis tests on single means and single proportions. You will also learn about the errors associated with these tests.

Null and Alternative Hypotheses

The actual test begins by considering two hypotheses. They are called the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints.

: The null hypothesis: It is a statement of no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

: The alternative hypothesis: It is a claim about the population that is contradictory to and what we conclude when we cannot accept . The alternative hypothesis is the contender and must win with significant evidence to overthrow the status quo. This concept is sometimes referred to the tyranny of the status quo because as we will see later, to overthrow the null hypothesis takes usually 90 or greater confidence that this is the proper decision.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “cannot accept ” if the sample information favors the alternative hypothesis or “fail to reject ” if the sample information is insufficient to reject the null hypothesis. These conclusions are all based upon a level of probability, a significance level, that is set my the analyst.

Table 1 presents the various hypotheses in the relevant pairs. For example, if the null hypothesis is equal to some value, the alternative has to be not equal to that value.

equal (=)	not equal (≠)
greater than or equal to (≥)	less than (<)
less than or equal to (≤)	more than (>)

Table 1

NOTE                                                                             

As a mathematical convention always has a symbol with an equal in it. never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test.

Example 1:

: No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

: More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

Example 2:

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

: = 2.0

: ≠ 2.0

Example 3:

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

: ≥ 5

: < 5

Outcomes and the Type I and Type II Errors

When you perform a hypothesis test, there are four possible outcomes depending on the actual truth (or falseness) of the null hypothesis and the decision to reject or not. The outcomes are summarized in Table 2:

STATISTICAL DECISION	IS ACTUALLY…
	True	False
Cannot reject	Correct Outcome	Type II error
Cannot accept	Type I Error	Correct Outcome

Table 2

1. The decision is cannot reject 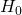 when 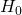is true (correct decision).
2. The decision is cannot accept 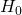when 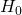is true (incorrect decision known as a Type I error). This case is described as “rejecting a good null”. As we will see later, it is this type of error that we will guard against by setting the probability of making such an error. The goal is to NOT take an action that is an error.
3. The decision is cannot reject 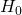when, in fact, 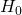is false (incorrect decision known as a Type II error). This is called “accepting a false null”. In this situation you have allowed the status quo to remain in force when it should be overturned. As we will see, the null hypothesis has the advantage in competition with the alternative.
4. The decision is cannot accept 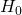when 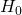is false (correct decision).

Each of the errors occurs with a particular probability. The Greek letters α and β represent the probabilities.

= probability of a Type I error = P(Type I error) = probability of rejecting the null hypothesis when the null hypothesis is true: rejecting a good null.

= probability of a Type II error = P(Type II error) = probability of not rejecting the null hypothesis when the null hypothesis is false. (1 − ) is called the Power of the Test.

and should be as small as possible because they are probabilities of errors.

Statistics allows us to set the probability that we are making a Type  I error.  The probability of making a Type  I error is . Recall that the confidence intervals in the last unit were set by choosing a value called (or ) and the value determined the confidence level of the estimate because it was the probability of the interval failing to capture the true mean (or proportion parameter p). This and that one are the same.

The easiest way to see the relationship between the error and the level of confidence is with the following figure (Figure 1).

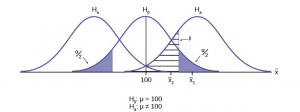
Figure 1

We can also see in Figure 1 that the sample mean could be really from an distribution, but within the boundary set by the alpha level. Such a case is marked as . There is a probability that actually came from but shows up in the range of between the two tails. This probability is the error, the probability of accepting a false null.

Our problem is that we can only set the error because there are an infinite number of alternative distributions from which the mean could have come that are not equal to . As a result, the statistician places the burden of proof on the alternative hypothesis. That is, we will not reject a null hypothesis unless there is a greater than 90, or 95, or even 99 percent probability that the null is false: the burden of proof lies with the alternative hypothesis. This is why we called this the tyranny of the status quo earlier.

By way of example, the American judicial system begins with the concept that a defendant is “presumed innocent”. This is the status quo and is the null hypothesis. The judge will tell the jury that they can not find the defendant guilty unless the evidence indicates guilt beyond a “reasonable doubt” which is usually defined in criminal cases as 95% certainty of guilt. If the jury cannot accept the null, innocent, then action will be taken, jail time. The burden of proof always lies with the alternative hypothesis. (In civil cases, the jury needs only to be more than 50% certain of wrongdoing to find culpability, called “a preponderance of the evidence”).

The example above was for a test of a mean, but the same logic applies to tests of hypotheses for all statistical parameters one may wish to test.

The following are examples of Type I and Type II errors.

Example 4

Suppose the null hypothesis,  , is: Frank’s rock climbing equipment is safe.

Type I error: Frank thinks that his rock climbing equipment may not be safe when, in fact, it really is safe.

Type II error: Frank thinks that his rock climbing equipment may be safe when, in fact, it is not safe.

= probability that Frank thinks his rock climbing equipment may not be safe when, in fact, it really is safe. = probability that Frank thinks his rock climbing equipment may be safe when, in fact, it is not safe.

Notice that, in this case, the error with the greater consequence is the Type II error. (If Frank thinks his rock climbing equipment is safe, he will go ahead and use it.)

This is a situation described as “accepting a false null”.

Example 5

Suppose the null hypothesis, , is: The victim of an automobile accident is alive when he arrives at the emergency room of a hospital. This is the status quo and requires no action if it is true. If the null hypothesis cannot be accepted then action is required and the hospital will begin appropriate procedures.

Type I error: The emergency crew thinks that the victim is dead when, in fact, the victim is alive. Type II error: The emergency crew does not know if the victim is alive when, in fact, the victim is dead.

= probability that the emergency crew thinks the victim is dead when, in fact, he is really alive = P(Type I error). = probability that the emergency crew does not know if the victim is alive when, in fact, the victim is dead = P(Type II error).

The error with the greater consequence is the Type I error. (If the emergency crew thinks the victim is dead, they will not treat him.)

Distribution Needed for Hypothesis Testing

Particular distributions are associated with hypothesis testing.We will perform hypotheses tests of a population mean using a normal distribution or a Student’s t-distribution. (Remember, use a Student’s t-distribution when the population standard deviation is unknown and the sample size is small, where small is considered to be less than 30 observations.) We perform tests of a population proportion using a normal distribution when we can assume that the distribution is normally distributed. We consider this to be true if the sample proportion, p ‘ , times the sample size is greater than 5 and 1- p ‘ times the sample size is also greater then 5. This is the same rule of thumb we used when developing the formula for the confidence interval for a population proportion.

Hypothesis Test for the Mean

Going back to the standardizing formula we can derive the test statistic for testing hypotheses concerning means.

The standardizing formula can not be solved as it is because we do not have , the population mean. However, if we substitute in the hypothesized value of the mean, in the formula as above, we can compute a Z value. This is the test statistic for a test of hypothesis for a mean and is presented in Figure 2. We interpret this Z value as the associated probability that a sample with a sample mean of could have come from a distribution with a population mean of and we call this Z value for “calculated”. Figure 2 and Figure 3 show this process.

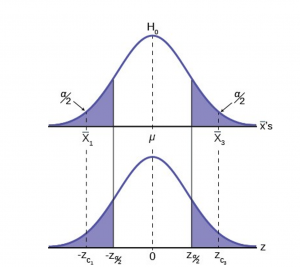
Figure 2

Notice that for each there is an associated , called the calculated Z, that comes from solving the equation above. This calculated Z is nothing more than the number of standard deviations that the hypothesized mean is from the sample mean. If the sample mean falls “too many” standard deviations from the hypothesized mean we conclude that the sample mean could not have come from the distribution with the hypothesized mean, given our pre-set required level of significance.  It could have come from , but it is deemed just too unlikely. In Figure 2 both  and are in the tails of the distribution. They are deemed “too far” from the hypothesized value of the mean given the chosen level of alpha. If in fact this sample mean it did come from , but from in the tail, we have made a Type I error: we have rejected a good null. Our only real comfort is that we know the probability of making such an error, , and we can control the size of .

Figure 3 shows the third possibility for the location of the sample mean, x . Here the sample mean is within the two critical values. That is, within the probability of (1-) and we cannot reject the null hypothesis.

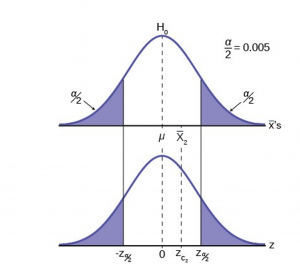
Figure 3

This gives us the decision rule for testing a hypothesis for a two-tailed test:

Decision Rule: Two-Tail Test

If : then cannot REJECT

If : then cannot ACCEPT

This rule will always be the same no matter what hypothesis we are testing or what formulas we are using to make the  test. The only change will be to change the to the appropriate symbol for the test statistic for the parameter being  tested. Stating the decision rule another way: if the sample mean is unlikely to have come from the distribution with the hypothesized mean we cannot accept the null hypothesis. Here we define “unlikely” as having a probability less than alpha of occurring.

P-Value Approach

An alternative decision rule can be developed by calculating the probability that a sample mean could be found that would give a test statistic larger than the test statistic found from the current sample data assuming that the null hypothesis is true. Here the notion of “likely” and “unlikely” is defined by the probability of drawing a sample with a mean from a population with the hypothesized mean that is either larger or smaller than that found in the sample data. Simply stated, the p-value approach compares the desired significance level, , to the p-value which is the probability of drawing a sample mean further from the hypothesized value than the actual sample mean. A large p-value calculated from the data indicates that we should not reject the null hypothesis. The smaller the p-value, the more unlikely the outcome, and the stronger the evidence is against the null hypothesis. We would reject the null hypothesis if the evidence is strongly against it. The relationship between the decision rule of comparing the calculated test statistics, , and the Critical Value, , and using the p-value can be seen in Figure 4.

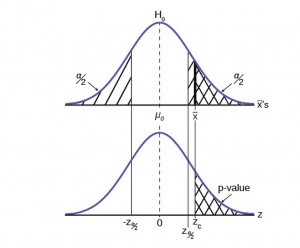
Figure 4

The calculated value of the test statistic is in this example and is marked on the bottom graph of the standard normal distribution because it is a Z value. In this case the calculated value is in the tail and thus we cannot accept the null hypothesis, the associated  is just too unusually large to believe that it came from the distribution with a mean of with a significance level of .

If we use the p-value decision rule we need one more step. We need to find in the standard normal table the probability associated with the calculated test statistic, . We then compare that to the α associated with our selected level of confidence. In Figure 4 we see that the p-value is less than and therefore we cannot accept the null. We  know that  the p-value is less than  because the area under the p-value is smaller than . It is important to note that two researchers drawing randomly from the same population may find two different p-values from their samples. This occurs because the p-value is calculated as the probability in the tail beyond the sample mean assuming that the null hypothesis is correct. Because the sample means will in all likelihood be different this will create two different p-values. Nevertheless, the conclusions as to the null hypothesis should be different with only the level of probability of .

Here is a systematic way to make a decision of whether you cannot accept or cannot reject a null hypothesis if using the p-value and a preset or preconceived (the ” significance level“). A preset α is the probability of a Type I error (rejecting the null hypothesis when the null hypothesis is true). It may or may not be given to you at the beginning of the problem. In any case, the value of is the decision of the analyst. When you make a decision to reject or not reject , do as follows:

•      If α > p-value, cannot accept . The results of the sample data are significant. There is sufficient evidence to conclude that is an incorrect belief and that the alternative hypothesis, , may be correct.

•      If α ≤ p-value, cannot reject . The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis, , may be correct. In this case the status quo stands.

• When you “cannot reject “, it does not mean that you should believe that is true. It simply means that the sample data have failed to provide sufficient evidence to cast serious doubt about the truthfulness of . Remember that the null is the status quo and it takes high probability to overthrow the status quo. This bias in favor of the null hypothesis is what gives rise to the statement “tyranny of the status quo” when discussing hypothesis testing and the scientific method.

Both decision rules will result in the same decision and it is a matter of preference which one is used.

One and Two-tailed Tests

The discussion of Figures 2-4 was based on the null and alternative hypothesis presented in Figure 2. This was called a two-tailed test because the alternative hypothesis allowed that the mean could have come from a population which was either larger or smaller than the hypothesized mean in the null hypothesis. This could be seen by the statement of the alternative hypothesis as , in this example.

It may be that the analyst has no concern about the value being “too” high or “too” low from the hypothesized value. If this is the case, it becomes a one-tailed test and all of the alpha probability is placed in just one tail and not split into /2 as in the above case of a two-tailed test. Any test of a claim will be a one-tailed test. For example, a car manufacturer claims that their Model 17B provides gas mileage of greater than 25 miles per gallon. The null and alternative hypothesis would be:

: ≤ 25

: > 25

The claim would be in the alternative hypothesis. The burden of proof in hypothesis testing is carried in the alternative. This is because failing to reject the null, the status quo, must be accomplished with 90 or 95 percent significance that it cannot be maintained. Said another way, we want to have only a 5 or 10 percent probability of making a Type I error, rejecting a good null; overthrowing the status quo.

This is a one-tailed test and all of the probability is placed in just one tail and not split into /2 as in the above case of a two-tailed test.

Figure 5 shows the two possible cases and the form of the null and alternative hypothesis that give rise to them.

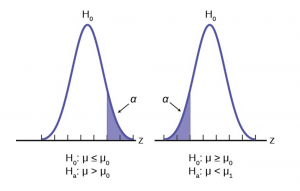
Figure 5

Effects of Sample Size on Test Statistic

In developing the confidence intervals for the mean from a sample, we found that most often we would not have the population standard deviation, σ. If the sample size were larger than 30, we could simply substitute the point estimate for , the sample standard deviation, s, and use the student’s t distribution to correct for this lack of information.

When testing hypotheses we are faced with this same problem and the solution is exactly the same. Namely: If the population standard deviation is unknown, and the sample size is less than 30, substitute s, the point estimate for the population standard deviation, , in the formula for the test statistic and use the student’s t distribution. All the formulas and figures above are unchanged except for this substitution and changing the Z distribution to the student’s t distribution on the graph. Remember that the student’s t distribution can only be computed knowing the proper degrees of freedom for the problem. In this case, the degrees of freedom is computed as before with confidence intervals: df = (n-1). The calculated t-value is compared to the t-value associated with the pre-set level of confidence required in the test, , df found in the student’s t tables. If we do not know , but the sample size is 30 or more, we simply substitute s for and use the normal distribution.

Table 3 summarizes test statistics for varying sample sizes and population standard deviation known and unknown.

Sample Size	Test Statistic
< 30 (σ unknown)
< 30 (σ known)
> 30 (σ unknown)
> 30 (σ known)

Table 3

A Systematic Approach for Testing A Hypothesis

A systematic approach to hypothesis testing follows the following steps and in this order. This template will work for all hypotheses that you will ever test.

• Set up the null and alternative hypothesis. This is typically the hardest part of the process. Here the question being asked is reviewed. What parameter is being tested, a mean, a proportion, differences in means, etc. Is this a one-tailed test or two-tailed test? Remember, if someone is making a claim it will always be a one-tailed test.
• Decide the level of significance required for this particular case and determine the critical value. These can be found in the appropriate statistical table. The levels of confidence typical for the social sciences are 90, 95 and 99. However, the level of significance is a policy decision and should be based upon the risk of making a Type I error, rejecting a good null. Consider the consequences of making a Type I error.

Next, on the basis of the hypotheses and sample size, select the appropriate test statistic and find the relevant critical value: , , etc. Drawing the relevant probability distribution and marking the critical value is always big help. Be sure to match the graph with the hypothesis, especially if it is a one-tailed test.

• Take a sample(s) and calculate the relevant parameters: sample mean, standard deviation, or proportion. Using the formula for the test statistic from above in step 2, now calculate the test statistic for this particular case using the parameters you have just calculated.
• Compare the calculated test statistic and the critical value. Marking these on the graph will give a good visual picture of the situation. There are now only two situations:

a.     The test statistic is in the tail: Cannot Accept the null, the probability that this sample mean (proportion) came from the hypothesized distribution is too small to believe that it is the real home of these sample data.

b.   The test statistic is not in the tail: Cannot Reject the null, the sample data are compatible with the hypothesized population parameter.

• Reach a conclusion. It is best to articulate the conclusion two different ways. First a formal statistical conclusion such as “With a 95 % level of significance we cannot accept the null hypotheses that the population mean is equal to XX (units of measurement)”. The second statement of the conclusion is less formal and states the action, or lack of action, required. If the formal conclusion was that above, then the informal one might be, “The machine is broken and we need to shut it down and call for repairs”.

All hypotheses tested will go through this same process. The only changes are the relevant formulas and those are determined by the hypothesis required to answer the original question.

Full Hypothesis Test Examples

Tests on Means

Example 6

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds. His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims. For the 15 swims, Jeffrey’s mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05.

Solution – Example 6

Set up the Hypothesis Test:

Since the problem is about a mean, this is a test of a single population mean. Set the null and alternative hypothesis:

In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test. The claim will always be in the alternative hypothesis because the burden of proof always lies with the alternative. Remember that the status quo must be defeated with a high degree of confidence, in this case 95 % confidence. The null and alternative hypotheses are thus:

: ≥ 16.43

: < 16.43

For Jeffrey to swim faster, his time will be less than 16.43 seconds. The “<” tells you this is left-tailed. Determine the distribution needed:

Random variable: = the mean time to swim the 25-yard freestyle.

Distribution for the test statistic:

The sample size is less than 30 and we do not know the population standard deviation so this is a t-test and the proper formula is:

= 16.43 comes from and not the data. = 16. s = 0.8, and n = 15.

Our step 2, setting the level of significance, has already been determined by the problem, .05 for a 95 % significance level. It is worth thinking about the meaning of this choice. The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.) For this case the only concern with a Type I error would seem to be that Jeffery’s dad may fail to bet on his son’s victory because he does not have appropriate confidence in the effect of the goggles.

To find the critical value we need to select the appropriate test statistic. We have concluded that this is a t-test on the basis of the sample size and that we are interested in a population mean. We can now draw the graph of the t-distribution and mark the critical value (Figure 6). For this problem the degrees of freedom are n-1, or 14. Looking up 14 degrees of freedom at the 0.05 column of the t-table we find 1.761. This is the critical value and we can put this on our graph.

Step 3 is the calculation of the test statistic using the formula we have selected.

We find that the calculated test statistic is 2.08, meaning that the sample mean is 2.08 standard deviations away from the hypothesized mean of 16.43.

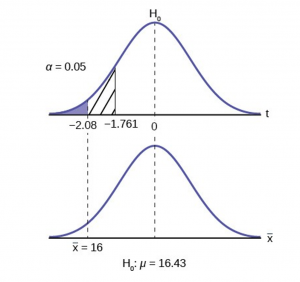
Figure 6

Step 4 has us compare the test statistic and the critical value and mark these on the graph. We see that the test statistic is in the tail and thus we move to step 4 and reach a conclusion. The probability that an average time of 16 minutes could come from a distribution with a population mean of 16.43 minutes is too unlikely for us to accept the null hypothesis. We cannot accept the null.

Step 5 has us state our conclusions first formally and then less formally. A formal conclusion would be stated as: “With a 95% level of significance we cannot accept the null hypothesis that the swimming time with goggles comes from a distribution with a population mean time of 16.43 minutes.” Less formally, “With 95% significance we believe that the goggles improves swimming speed”

If we wished to use the p-value system of reaching a conclusion we would calculate the statistic and take the additional step to find the probability of being 2.08 standard deviations from the mean on a t-distribution. This value is .0187. Comparing this to the α-level of .05 we see that we cannot accept the null. The p-value has been put on the graph as the shaded area beyond -2.08 and it shows that it is smaller than the hatched area which is the alpha level of 0.05. Both methods reach the same conclusion that we cannot accept the null hypothesis.

Example 7

Jane has just begun her new job as on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of $108 with a standard deviation of 12 dollars. Test at 5% significance that the population mean is at least $100 against the alternative that it is less than 100 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jane has met this requirement at the significance level of 95%?

Solution – Example 7

STEP 1: Set the Null and Alternative Hypothesis.

: ≤ 100

: > 100

The null and alternative hypothesis are for the parameter because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not “too high” a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis.

STEP 2: Decide the level of significance and draw the graph (Figure 7) showing the critical value.

Critical value: with n-1 degrees of freedom= 15

 

 

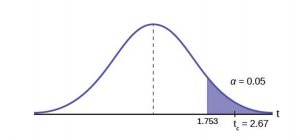
Figure 7

STEP 3: Calculate sample parameters and the test statistic.

=

STEP 4: Compare test statistic and the critical values

STEP 5: Reach a Conclusion

The test statistic is a Student’s t because the sample size is below 30; therefore, we cannot use the normal distribution. Comparing the calculated value of the test statistic and the critical value of t (ta) at a 5% significance level, we see that the calculated value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we cannot accept the null hypothesis. There is evidence that supports Jane’s performance meets company standards.

Example 8

A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, . Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of significance in the analysis should be 99%.

Again we will follow the steps in our analysis of this problem.

Solution – Example 8

STEP 1: Set the Null and Alternative Hypothesis. The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:

: =  8

: ≠ 8

STEP 2: Decide the level of significance and draw the graph showing the critical value.

This problem has already set the level of significance at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because this is a continuous random variable and we are interested in the mean, and the sample size is greater than 30, the appropriate distribution is the normal distribution and the relevant critical value is 2.575 from the normal table or the t-table at 0.005 column and infinite degrees of freedom. We draw the graph and mark these points (Figure 8).

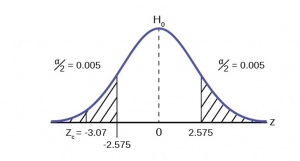
Figure 8

STEP 3: Calculate sample parameters and the test statistic. The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, s, is 0.173. With this information we calculate the test statistic as -3.07, and mark it on the graph.

STEP 4: Compare test statistic and the critical values Now we compare the test statistic and the critical value by placing the test statistic on the graph. We see that the test statistic is in the tail, decidedly greater than the critical value of 2.575. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard deviations. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3 plus standard deviations away and thus we cannot accept the null hypothesis.

STEP 5: Reach a Conclusion

Three standard deviations of a test statistic will guarantee that the test will fail. The probability that anything is within three standard deviations is almost zero. Actually it is 0.0026 on the normal distribution, which is certainly almost zero in a practical sense. Our formal conclusion would be “ At a 99% level of significance we cannot accept the hypothesis that the sample mean came from a distribution with a mean of 8 ounces” Or less formally, and getting to the point, “At a 99% level of significance we conclude that the machine is under filling the bottles and is in need of repair”.