Where is the sample mean.   is determined by the level of confidence desired by the analyst, and is the standard deviation of the sampling distribution for means.

A Confidence Interval for a Population Standard Deviation, Known or Large Sample Size

A confidence interval for a population mean with a known population standard deviation is based on the conclusion  that the sampling distribution of the sample means follow an approximately normal distribution.

Calculating the Confidence Interval

To construct a confidence interval for a single unknown population mean , where the population standard deviation is known, we need x as an estimate for and we need the margin of error. Here, the margin of error is called the error bound for a population mean (abbreviated EBM). The sample mean x is the point estimate of the unknown population mean.

To construct a confidence interval estimate for an unknown population mean we need data from a random sample. The steps to construct and interpret the confidence interval are:

• Calculate the sample mean x from the sample data. Remember in this section we already know the population standard deviation, .
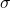• Find the Z-score that corresponds to the confidence level.
• Calculate the error bound EBM.
• Construct the confidence interval.
• Write a sentence that interprets the estimate in the context of the situation in the problem. (Explain what the confidence interval means1 in the words of the problem.)

Finding the z-score for the Stated Confidence Level

When we know the population standard deviation , we use a standard normal distribution to calculate the error bound EBM and construct the confidence interval. We need to find the value of z that puts an area equal to the confidence level (in decimal form) in the middle of the standard normal distribution Z ~ N(0, 1).

Calculating the Error Bound (EBM)

The error bound formula for an unknown population mean when the population standard deviation is known is

• EBM =

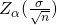
Constructing the Confidence Interval

The confidence interval estimate has the format (-EBM, +EBM).

A good way to see the development of a confidence interval is to graphically depict the solution to a problem requesting   a confidence interval. This is presented in Figure 2 for the example in the introduction concerning the number of downloads from iTunes. That case was for a 95% confidence interval, but other levels of confidence could have just as easily been chosen depending on the need of the analyst. However, the level of confidence MUST be pre-set and not subject to revision as a result of the calculations.

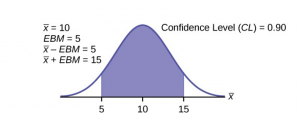
Figure 2

For this example, let’s say we know that the actual population mean number of iTunes downloads is 2.1. The true population mean falls within the range of the 95% confidence interval. There is absolutely nothing to guarantee that this will happen. Further, if the true mean falls outside of the interval we will never know it. We must always remember that we will never ever know the true mean. Statistics simply allows us, with a given level of probability (confidence), to say that the true mean is within the range calculated. This is what we will call the “level of ignorance admitted”.

Changing the Confidence Level or Sample Size

Here again is the formula for a confidence interval for an unknown population mean assuming we know the population standard deviation:

–

It is clear that the confidence interval is driven by two things, the chosen level of confidence, , and the standard deviation of the sampling distribution. The standard deviation of the sampling distribution is further affected by two things, the standard deviation of the population and the sample size we chose for our data. Here we wish to examine the effects of each of the choices we have made on the calculated confidence interval, the confidence level and the sample size.

For a moment we should ask just what we desire in a confidence interval. Our goal was to estimate the population mean from a sample. We have forsaken the hope that we will ever find the true population mean, and population standard deviation for that matter, for any case except where we have an extremely small population and the cost of gathering the data of interest is very small. In all other cases we must rely on samples. We have the tools to provide a meaningful confidence interval with a given level of confidence, meaning a known probability of being wrong. By meaningful confidence interval we mean one that is useful.

Imagine that you are asked for a confidence interval for the ages of your classmates. You have taken a sample and find a mean of 19.8 years. You wish to be very confident so you report an interval between 9.8 years and 29.8 years. This interval would certainly contain the true population mean and have a very high confidence level. However, it hardly qualifies as meaningful. The very best confidence interval is narrow while having high confidence. There is a natural tension between these two goals. The higher the level of confidence the wider the confidence interval as the case of the students’ ages above. We can see this tension in the equation for the confidence interval:

=

The confidence interval will increase in width as increases, increases as the level of confidence increases. There is a tradeoff between the level of confidence and the width of the interval. Now let’s look at the formula again and we see that the sample size also plays an important role in the width of the confidence interval. The sample sized,  n , shows up in the denominator of the standard deviation of the sampling distribution. As the sample size increases, the standard deviation of the sampling distribution decreases and thus the width of the confidence interval, while holding constant the level of confidence. Again we see the importance of having large samples for our analysis although we then face a second constraint, the cost of gathering data.

Example 1

Solution – Example 1

To find the confidence interval, you need the sample mean, and the EBM.

= 68

EBM =

=3 n=36; The confidence level is 90% (CL = 0.90)

CL = 0.90 so = 1 – CL = 1 – 0.90 = 0.10

= 0.05 =

 

The area to the right of    is 0.05 and the area to the left of   is 1 – 0.05 = 0.95.

= = 1.645

This can be found using a computer, or using a probability table for the standard normal distribution. Because the common levels of confidence in the social sciences are 90%, 95% and 99% it will not be long until you become familiar with the numbers , 1.645, 1.96, and 2.56.

EBM = = 0.8225

– EBM = 68 – 0.8225 = 67.1775

+ EBM = 68 + 0.8225 = 68.8225

The 90% confidence interval is (67.1775, 68.8225).

Interpretation

 We estimate with 90% confidence that the true population mean exam score for all statistics students is between 67.18 and 68.82.

Find a 90% confidence interval for the true (population) mean of statistics exam scores.

Suppose we change the original problem in Example 1 by using a 95% confidence level. Find a 95% confidence interval for the true (population) mean statistics exam score.

Example 2

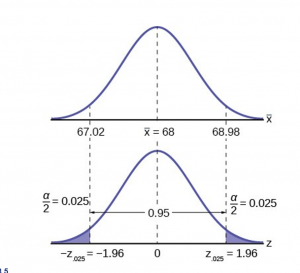
Figure 3

= 3; n = 36; The confidence level is 95% (CL = 0.95).

CL = 0.95 so α = 1 – CL = 1 – 0.95 = 0.05

= = 1.96

EBM = = 0.98

– EBM = 68 – 0.98 = 67.1775

+ EBM = 68 + 0.98 = 68.8225

The 95% confidence interval is (67.02, 68.98).

67.02 68.98

Notice that the EBM is larger for a 95% confidence level in the original problem. As a result, the confidence interval is larger.

Comparing the results

The 90% confidence interval is (67.18, 68.82). The 95% confidence interval is (67.02, 68.98). The 95% confidence interval is wider. If you look at the graphs, because the area 0.95 is larger than the area 0.90, it makes sense that the 95% confidence interval is wider. To be more confident that the confidence interval actually does contain the true value of the population mean for all statistics exam scores, the confidence interval necessarily needs to be wider. This demonstrates a very important principle of confidence intervals. There is a trade off between the level of confidence and the width of the interval. Our desire is to have a narrow confidence interval, huge wide intervals provide little information that is useful. But we would also like to have a high level of confidence in our interval. This demonstrates that we cannot have both.

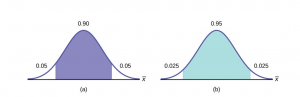
Figure 4

Summary: Effect of Changing the Confidence Level

• Increasing the confidence level makes the confidence interval wider.
• Decreasing the confidence level makes the confidence interval narrower.

Suppose we change the original problem in Example 1 to see what happens to the confidence interval if the sample size is changed.

Example 3

Leave everything the same except the sample size. Use the original 90% confidence level. What happens to the confidence interval if we increase the sample size and use n = 100 instead of n = 36? What happens if we decrease the sample size to n = 25 instead of n = 36?

= 3; n = 100; The confidence level is 90% (CL = 0.90).

CL = 0.90 so = 1 – CL = 1 – 0.90 = 0.10

= = 1.645

EBM = = 0.492

– EBM = 68 – 0.492 = 67.5065

+ EBM = 68 + 0.492 = 68.4935

The 90% confidence interval is (67.51, 68.49).

67.51 68.49

If we increase the sample size n to 100, we decrease the width of the confidence interval relative to the original sample size of 36 observations.

= 3; n = 25; The confidence level is 90% (CL = 0.90).

CL = 0.90 so = 1 – CL = 1 – 0.90 = 0.10

= = 1.645

EBM = = 0.987

– EBM = 68 – 0.987= 67.013

+ EBM = 68 + 0.987 = 68.987

The 90% confidence interval is (67.013, 68.987).

67.013  68.987

If we decrease the sample size n to 25, we increase the width of the confidence interval by comparison to the original sample size of 36 observations.

Summary: Effect of Changing the Sample Size

• Increasing the sample size makes the confidence interval narrower.
• Decreasing the sample size makes the confidence interval wider.

 

Thus far we assumed that we knew the population standard deviation. This will virtually never be the case. We will have the sample standard deviation, s, however. This is a point estimate for the population standard deviation and can be substituted into the formula for confidence intervals for a mean under certain circumstances. When the sample size is large “enough” we can invoke the Central Limit Theorem to substitute the point estimate for the standard deviation. Simulation studies indicate that 30 observations or more will be sufficient to eliminate any meaningful bias in the estimated confidence interval.

 A Confidence Interval for a Population Standard Deviation Unknown, Small Sample Case

Up until the mid-1970s, some statisticians used the normal distribution approximation for large sample sizes and used the Student’s t-distribution only for sample sizes of at most 30 observations.

If you draw a simple random sample of size n from a population with mean and unknown population standard deviation  and calculate the t-score , then the t-scores follow a Student’s t-distribution with n – 1 degrees of freedom. The t-score has the same interpretation as the z-score. It measures how far in standard deviation units x– is from its mean . For each sample size n, there is a different Student’s t-distribution. The degrees of freedom, n – 1, come from the calculation of the sample standard deviation s. Remember when we first calculated a sample standard deviation we divided the sum of the squared deviations by n − 1, but we used n deviations ( values) to calculate s. Because the sum of the deviations is zero, we can find the last deviation once we know the other n – 1 deviations. The other n – 1 deviations can change or vary freely. We call the number n – 1 the degrees of freedom (df) in recognition that one is lost in the calculations. The effect of losing a degree of freedom is that the t-value increases and the confidence interval increases in width.

Properties of the Student’s t-Distribution

• The graph for the Student’s t-distribution is similar to the standard normal curve and at infinite degrees of freedom it is the normal distribution. You can confirm this by reading the bottom line at infinite degrees of freedom for a familiar level of confidence, e.g. at column 0.05, 95% level of confidence, we find the t-value of 1.96 at infinite degrees of freedom.
• The mean for the Student’s t-distribution is zero and the distribution is symmetric about zero, again like the standard normal distribution.
• The Student’s t-distribution has more probability in its tails than the standard normal distribution because the spread of the t-distribution is greater than the spread of the standard normal. So the graph of the Student’s t-distribution will be thicker in the tails and shorter in the center than the graph of the standard normal distribution.
• The exact shape of the Student’s t-distribution depends on the degrees of freedom. As the degrees of freedom increases, the graph of Student’s t-distribution becomes more like the graph of the standard normal distribution.
• The underlying population of individual observations is assumed to be normally distributed with unknown population mean μ and unknown population standard deviation σ. This assumption comes from the Central Limit theorem because the individual observations in this case are the 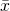 s of the sampling distribution. The size of the underlying population is generally not relevant unless it is very small. If it is normal then the assumption is met and doesn’t need discussion.

A probability table for the Student’s t-distribution is used to calculate t-values at various commonly-used levels of confidence. The table gives t-scores that correspond to the confidence level (column) and degrees of freedom (row). When using a t-table, note that some tables are formatted to show the confidence level in the column headings, while the column headings in some tables may show only corresponding area in one or both tails. Notice that at the bottom the table will show the t-value for infinite degrees of freedom. Mathematically, as the degrees of freedom increase, the t distribution approaches the standard normal distribution. You can find familiar Z-values by looking in the relevant alpha column and reading value in the last row.

A Student’s t table  gives t-scores given the degrees of freedom and the right-tailed probability.

The Student’s t distribution has one of the most desirable properties of the normal: it is symmetrical. What the Student’s t distribution does is spread out the horizontal axis so it takes a larger number of standard deviations to capture the same amount of probability. In reality there are an infinite number of Student’s t distributions, one for each adjustment to the sample size. As the sample size increases, the Student’s t distribution become more and more like the normal distribution. When the sample size reaches 30 the normal distribution is usually substituted for the Student’s t because they are so much alike. This relationship between the Student’s t distribution and the normal distribution is shown in Figure 5.

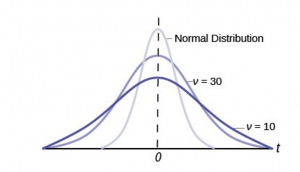
Figure 5

This is another example of one distribution limiting another one, in this case the normal distribution is the limiting distribution of the Student’s t when the degrees of freedom in the Student’s t approaches infinity. This conclusion comes directly from the derivation of the Student’s t distribution by Mr. Gosset. He recognized the problem as having few observations and no estimate of the population standard deviation. He was substituting the sample standard deviation and getting volatile results. He therefore created the Student’s t distribution as a ratio of the normal distribution and Chi squared distribution. The Chi squared distribution is itself a ratio of two variances, in this case the sample variance and the unknown population variance. The Student’s t distribution thus is tied to the normal distribution, but has degrees of freedom that come from those of the Chi squared distribution.

Restating the formula for a confidence interval for the mean for cases when the sample size is smaller than 30 and we do not know the population standard deviation:

–

Here the point estimate of the population standard deviation, s has been substituted for the population standard deviation, , and has been substituted for . The Greek letter (pronounced nu) is placed in the general formula in recognition that there are many Student distributions, one for each sample size. is the symbol for the degrees of freedom of the distribution and depends on the size of the sample. Often df is used to abbreviate degrees of freedom. For this type of problem, the degrees of freedom is = n-1, where n is the sample size. To look up a probability in the Student’s t table we have to know the degrees of freedom in the problem.

Example 4

The average earnings per share (EPS) for 10 industrial stocks randomly selected from those listed on the Dow- Jones  Industrial  Average  was  found  to  be =  1.85  with  a  standard  deviation  of  s=0.395.  Calculate  a  99% confidence interval for the average EPS of all the industrials listed on the DJIA.

–

Solution – Example 4

To help visualize the process of calculating a confident interval we draw the appropriate distribution for the problem. In this case this is the Student’s t because we do not know the population standard deviation and the sample is small, less than 30.

Figure 6

To find the appropriate t-value requires two pieces of information, the level of confidence desired and the degrees of freedom. The question asked for a 99% confidence level. On the graph this is shown where (1-) , the level  of confidence , is in the unshaded area. The tails, thus, have .005 probability each, /2. The degrees of freedom for this type of problem is n-1= 9. From the Student’s t table, at the row marked 9 and column marked .005, is the number of standard deviations to capture 99% of the probability, 3.2498. These are then placed on the graph remembering that the Student’s t is symmetrical and so the t-value is both plus or minus on each side of the mean.

Inserting these values into the formula gives the result. These values can be placed on the graph to see the relationship between the distribution of the sample means,  ‘s and the Student’s t distribution.

=

1.445 2.257