The Normal Distribution

Margo Bergman

9 The Normal Distribution

Student Learning Outcomes

By the end of this chapter, the student should be able to:

Recognize the normal probability distribution and apply it appropriately.
Recognize the standard normal probability distribution and apply it appropriately.
Compare normal probabilities by converting to the standard normal distribution.

Introduction

The normal, a continuous distribution, is the most important of all the distributions. It is widely used and even more widely abused. Its graph is bell-shaped. You see the bell curve in almost all disciplines. Some of these include psychology, business, economics, the sciences, nursing, and, of course, mathematics. Some of your instructors may use the normal distribution to help determine your grade. Most IQ scores are normally distributed. Often real estate prices fit a normal distribution. The normal distribution is extremely important but it cannot be applied to everything in the real world.

In this chapter, you will study the normal distribution, the standard normal, and applications associated with them.

The normal distribution has two parameters (two numerical descriptive measures), the mean ( $\mu$ ) and the standard deviation ( $\sigma$ ). If X is a quantity to be measured that has a normal distribution with mean ( $\mu$ ) and the standard deviation ( $\sigma$ ), we designate this by writing:

NORMAL: $X \sim N \:(\mu, \sigma)$

Figure 1 shows the graph of a generic normal distribution, also known as the “bell curve”.

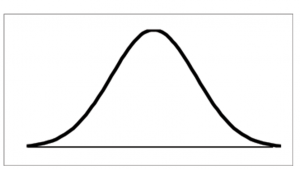
NormalDistribution

Figure 1

The probability density function is a rather complicated function. Do not memorize it. It is not necessary.

$f(x)=\frac{1}{\sigma\cdot\sqrt{2\cdot\pi}}$ $\cdot$ $e^{\frac{-1}{2}\cdot(\frac{x-\mu}{\sigma})^2}$ ${-1/2}\cdot(\frac{x-\mu}{\sigma})^2$

The cumulative distribution function is $P(X<x)$ . It is calculated either by a calculator or a computer or it is looked up in a table. Technology has made the tables basically obsolete. For that reason, as well as the fact that there are various table formats, we are not including table instructions in this chapter.

The curve is symmetrical about a vertical line drawn through the mean, $\mu$ . In theory, the mean is the same as the median since the graph is symmetric about $\mu$ . As the notation indicates, the normal distribution depends only on the mean and the standard deviation. Since the area under the curve must equal one, a change in the standard deviation, $\sigma$ , causes a change in the shape of the curve; the curve becomes fatter or skinnier depending on $\sigma$ . A change in $\mu$ causes the graph to shift to the left or right. This means there are an infinite number of normal probability distributions. One of special interest is called the standard normal distribution.

The Standard Normal Distribution

The standard normal distribution is a normal distribution of standardized values called z-scores. A z-score is measured in units of the standard deviation. For example, if the mean of a normal distribution is 5 and the standard deviation is 2, the value 11 is 3 standard deviations above (or to the right of) the mean. The calculation is:

$x=\mu+(z)\sigma=5+(3)(2)=11$

The z-score is 3.

The mean for the standard normal distribution is 0 and the standard deviation is 1. The transformation $z=\frac{x-\mu}{\sigma}$ produces the distribution $Z \sim N \:(0, 1)$ .

The value x comes from a normal distribution with mean $\mu$ and standard deviation $\sigma$ .

Z-scores

If X is a normally distributed random variable and $X \sim N \:(\mu, \sigma)$ , then the z-score is:

$z=\frac{x-\mu}{\sigma}$

The z-score tells you how many standard deviations that the value x is above (to the right of) or below (to the left of) the mean, $\mu$ . Values of x that are larger than the mean have positive z-scores and values of x that are smaller than the mean have negative z-scores. If x equals the mean, then x has a z-score of 0.

Example 1

Suppose $X \sim N \:(5, 6)$ . This says that X is a normally distributed random variable with mean $\mu$ = 5 and standard deviation $\sigma$ = 6. Suppose x = 17. Then:

$z=\frac{x-\mu}{\sigma} = \frac{17-5}{6}=2$

This means that x = 17 is 2 standard deviations (2 $\sigma$ ) above or to the right of the mean $\mu$ = 5. The standard deviation is $\sigma$ = 6.

Notice that:

5 + 2 · 6 = 17 (The pattern is $\mu$ + z $\sigma$ = x.)

Now suppose x = 1. Then:

$z=\frac{x-\mu}{\sigma} = \frac{1-5}{6}=-0.67$

(rounded to two decimal places)

This means that x = 1 is 0.67 standard deviations(-0.67 $\sigma$ )below or to the left of the mean $\mu=5$

5 + (−0.67) (6) is approximately equal to 1

(This has the pattern $\mu$ + (−0.67) $\sigma$ = 1 )

Summarizing, when z is positive, x is above or to the right of $\mu$ and when z is negative, x is to the left of or below $\mu$ .

Example 2

Some teachers believe that students can increase their grades 5 points, on the average, by studying for a month consistently. Suppose grades have a normal distribution. Let X = the amount of grade increase (in points) by a person in a month. Use a standard deviation of 2 points. $X \sim N \:(5, 2)$ . Fill in the blanks.

Problem 2.1

Suppose a person lost 10 points in a month. The z-score when x = 10 points is z = -2.5 (verify). This z-score tells you that x = 10 is standard deviations to the (right or left) of the mean (What is the mean?).

Problem 2.2

Suppose a person gained 3 point. Then z = . This z-score tells you that x = −3 is standard deviations to the (right or left) of the mean. Suppose the random variables X and Y have the following normal distributions: $X \sim N \:(5, 6)$ and $Y \sim N \:(2, 1)$ . If x = 17, then z = 2. (This was previously shown.) If y = 4, what is z?

The Empirical Rule

If X is a random variable and has a normal distribution with mean $\mu$ and standard deviation $\sigma$ then the

Empirical Rule says (See Figure 2 below)

About 68.27% of the x values lie between -1 $\sigma$ and +1 $\sigma$ of the mean $\mu$ (within 1 standard deviation of the mean).

About 95.45% of the x values lie between -2 $\sigma$ and +2 $\sigma$ of the mean $\mu$ (within 2 standard deviations of the mean).

About 99.73% of the x values lie between -3 $\sigma$ and +3 $\sigma$ of the mean $\mu$ (within 3 standard deviations of the mean). Notice that almost all the x values lie within 3 standard deviations of the mean.

The z-scores for +1 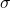$\sigma$ and –1 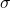$\sigma$ are +1 and -1, respectively.
The z-scores for +2 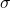$\sigma$ and –2 $\sigma$ are +2 and -2, respectively.
The z-scores for +3 $\sigma$ and –3 $\sigma$ are +3 and -3 respectively.

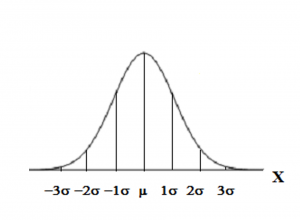
Figure 2

The Empirical Rule is also known as the 68-95-99.7 Rule.

Example 3

Suppose X has a normal distribution with mean 50 and standard deviation 6.

About 68.27% of the x values lie between -1 $\sigma$ = (-1)(6) = -6 and 1 $\sigma$ = (1)(6) = 6 of the mean 50. The values 50 – 6 = 44 and 50 + 6 = 56 are within 1 standard deviation of the mean 50. The z-scores are -1 and +1 for 44 and 56, respectively.

About 95.45% of the x values lie between -2 $\sigma$ = (-2)(6) = -12 and 2 $\sigma$ = (2)(6) = 12 of the mean 50.

The values 50 – 12 = 38 and 50 + 12 = 62 are within 2 standard deviations of the mean 50. The z-scores are -2 and 2 for 38 and 62, respectively.

About 99.73% of the x values lie between -3 $\sigma$ = (-3)(6) = -18 and 3 $\sigma$ = (3)(6) = 18 of the mean 50.

The values 50 – 18 = 32 and 50 + 18 = 68 are within 3 standard deviations of the mean 50. The z-scores are -3 and +3 for 32 and 68, respectively.

Areas to the Left and Right of X

The arrow in the graph below points to the area to the left of x. This area is represented by the probability

P (X < x). Normal tables, computers, and calculators provide or calculate the probability P (X < x).

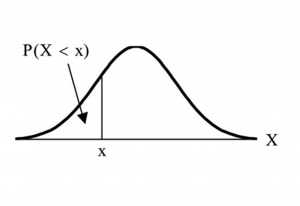
Figure 3

The area to the right is then P (X > x) = 1 − P (X < x).

Remember, P (X < x) = Area to the left of the vertical line through x.

P (X > x) = 1 − P (X < x) =. Area to the right of the vertical line through x

P (X < x) is the same as P (X ≤ x) and P (X > x) is the same as P (X ≥ x) for continuous distributions.

Calculations of Probabilities

Probabilities are calculated by using technology. There are instructions in the chapter for the TI-83+ and TI-84 calculators.

Example 4

If the area to the left is 0.0228, then the area to the right is 1 − 0.0228 = 0.9772.

Example 5

The final exam scores in a statistics class were normally distributed with a mean of 63 and a standard deviation of 5.

Problem 5.1

Find the probability that a randomly selected student scored more than 65 on the exam.

Solution 5.1

Let X = a score on the final exam. $X \sim N \:(63, 5)$ , where $\mu$ = 63 and $\sigma$ = 5

Draw a graph.

Then, find P (x > 65).

P (x > 65) = 0.3446 (calculator or computer)

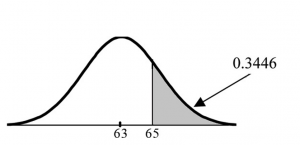
Figure 4

The probability that one student scores more than 65 is 0.3446.

Before technology, the z-score was looked up in a standard normal probability table (because the math involved is too cumbersome) to find the probability. In this example, a standard normal table with area to the left of the z-score was used. You calculate the z-score and look up the area to the left. The probability is the area to the right.

$z=\frac{65-63}{5} = 0.4$

Area to the left is 0.6554. P (x > 65) = P (z > 0.4) = 1 − 0.6554 = 0.3446

Problem 5.2

Find the probability that a randomly selected student scored less than 85.

Solution 5.2

Draw a graph.

Then find P (x < 85). Shade the graph. P (x < 85) = 1 (calculator or computer)

The probability that one student scores less than 85 is approximately 1 (or 100%).

The TI-instructions and answer are as follows:

normalcdf(0,85,63,5) = 1 (rounds to 1)

Problem 5.3

Find the 90th percentile (that is, find the score k that has 90 % of the scores below k and 10% of the scores above k).

Solution 5.3

Find the 90th percentile. For each problem or part of a problem, draw a new graph. Draw the x-axis. Shade the area that corresponds to the 90th percentile.

Let k = the 90th percentile. k is located on the x-axis. P (x < k) is the area to the left of k. The 90th percentile k separates the exam scores into those that are the same or lower than k and those that are the same or higher. Ninety percent of the test scores are the same or lower than k and 10% are the same or higher. k is often called a critical value.

k = 69.4 (calculator or computer)

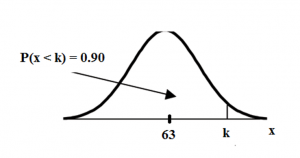
Figure 5

The 90th percentile is 69.4. This means that 90% of the test scores fall at or below 69.4 and 10% fall at or above. (0.90,63,5) = 69.4

Example 6

A computer is used for office work at home, research, communication, personal finances, education, entertainment, social networking and a myriad of other things. Suppose that the average number of hours a household personal computer is used for entertainment is 2 hours per day. Assume the times for entertainment are normally distributed and the standard deviation for the times is half an hour.

Problem 6.1

Find the probability that a household personal computer is used between 1.8 and 2.75 hours per day.

Solution 6.1

Let X = the amount of time (in hours) a household personal computer is used for entertainment.

$X \sim N \:(2, 0.5)$ where $\mu = 2$ and $\sigma = 0.5$

Find P (1.8 < x < 2.75).

The probability for which you are looking is the area between x=1.8 and x=2.75.

P (1.8 < x < 2.75) = 0.5886

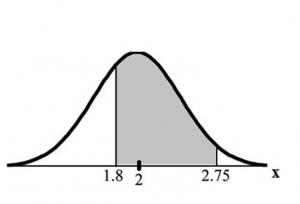
Figure 6

normalcdf(1.8,2.75,2,0.5) = 0.5886

The probability that a household personal computer is used between 1.8 and 2.75 hours per day for entertainment is 0.5886.

Problem 6.2

Find the maximum number of hours per day that the bottom quartile of households use a personal computer for entertainment.

Solution 6.2

To find the maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment, find the 25th percentile, k, where P (x < k) = 0.25.

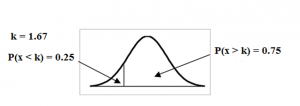
Figure 7

Media Attributions

NormalDist
EmpiricalRule
AreaUnderCurve
ProbProb1
ProbProb3
ProbProb6
ProbProb7

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License