Action Potential, Threshold, Refractory Period

Overview

This chapter:  (1) introduces the action potential and some of its key properties; (2) reviews the key aspects of electrical signaling that provide the mechanistic basis of the action potential; and (3) explains the action potential by stepping through the learning objectives. The Action Potential, Propagation chapter builds on these ideas to understand how action potentials propagate down axons to carry signals long distances.

Key properties of action potentials

A nerve cell has a negative membrane potential at rest – meaning the inside of the cell has an excess of negative charge. If we inject a weak, brief depolarizing current (i.e. an inward movement of positive charge, making the membrane potential less negative) into such a cell, we don’t see much interesting; specifically, the voltage changes smoothly in response and generally follows the shape of the injected current (Figure 1, far left trace). As we increase the magnitude of the injected current, at some point something very different happens (Figure 1, second trace from left): the membrane voltage makes a large and rapid excursion in response to injected current. This is an action potential – a large, rapid and discrete (i.e. stereotyped) change in membrane voltage. Action potentials are the basic unit of signaling in the central nervous system. All the information our brain receives about the sensory world, all the thoughts and dreams generated in the brain, and all the signals sent from the brain to muscles to generate motor outputs are conveyed via action potentials.

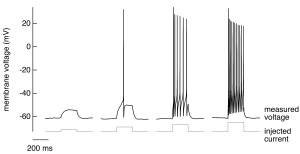
A key role of action potentials is transmitting signals over long distances with minimal delay. The sensory signals that initiate a spinal reflex, for example, can travel the ~1 m distance from your finger tips to the spinal cord in ~10 ms; likewise, a signal from the spinal cord can travel to a muscle in the arm to elicit a reaction to a sensory input in ~10 ms. Propagation of these signals without action potentials would take seconds rather than milliseconds, and hence spinal reflexes would be slowed tremendously without action potentials. Even for cells without long axons, action potentials can provide the voltage change needed to control other voltage-dependent cellular processes, such as the opening of voltage-gated calcium channels and associated events like exocytosis.

We will focus on several key properties of action potentials:

1. Individual action potentials are all-or-none events — they occur once the voltage exceeds a threshold level, and once triggered they are stereotyped — i.e. their shape does not depend on the stimulus that generated them (Figure 1).
2. The number of action potentials generated scales with the strength of the stimulus (the current injected into the cell in Figure 1 increases from left to right).
3. Action potentials propagate rapidly down axons, at speeds up to 100 m/s (see also Action Potential, Propagation).
4. Action potentials are generated by the opening and closing of ion channels in the cell membrane, and hence our understanding will be based in the properties of these channels. Mutations in these same channels cause of a number of inherited diseases. This should not be surprising given the importance of action potentials in signaling.

Quick review of membranes, ions and channels

(see also the chapters on Membrane Transport and Membrane Potentials)

Electrical signaling relies on concentration gradients of charged ions across the cell membrane. The membrane itself is impermeable to these charged ions. Ion channels — integral membrane proteins with a water-filled pore — provide the primary route for ions to cross the membrane. Channels are typically opened by intracellular or extracellular ligands. The opening of some ion channels — and in particular the Na⁺ and K⁺ channels that produce the action potential — depends on the membrane voltage. Most ion channel types do not exhibit such voltage dependence, but as we will see below it is absolutely essential for action potential generation. Finally, the selectivity of channels for specific ions — e.g. Na⁺ or K⁺ — together with differences in the distribution of these ions across the membrane accounts for differences in how the membrane voltage reacts to the opening of these channels (and hence to stimuli that cause the channels to open). The distribution of ions is captured by the equilibrium potential for that ion: key approximate values for our discussion are E_K ~ -100 mV, E_Cl ~ -90 mV, E_Na ~ +70 mV.

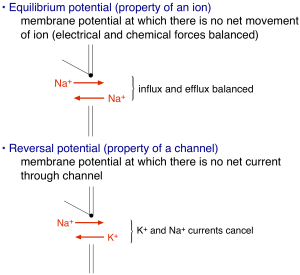
The amount of current flowing through an open ion channel is proportional to the difference between the membrane voltage and the reversal potential determined by the ion selectivity of the channel (no net current flows when the voltage is equal to the reversal potential, see Figure 2). The proportionality between the current and the voltage “driving force” is given by the channel’s conductance – i.e. I = G(V-V_rev) where I is the current, G is the conductance, V is the voltage and V_rev is the reversal potential, and the difference between the voltage and reversal potential, V-V_rev, is the driving force. This is Ohm’s law applied to an ion channel. Ohm’s law is probably more familiar as V = IR, where R is the resistance. Ohm’s law can be rewritten as V = I/G, from which you see that the conductance is simply the inverse of the resistance (i.e. if current flows easily, the resistance is low and the conductance is high). If it helps, you can think of an analogy with a water pipe: a large pipe that lets water flow easily has high conductance and low resistance, and the driving force is analogous to the water pressure – i.e. how hard are ions being pushed through the channel. The number of open channels, the voltage driving force, and the single channel conductance determine the magnitude of the total current flowing into or out of a cell through a specific channel type. Thus, these are the key parameters that will control electrical signaling.

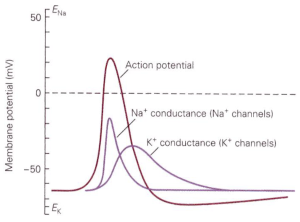
How do ion channels influence membrane voltage? The simple rule is that the flow of ions through a channel changes the voltage towards the reversal potential for that channel — i.e. the voltage at which there is no net movement of ions (Figure 2). For perfectly selective channels, this reversal potential occurs at the ion’s equilibrium potential. This description alone is enough to get us to a simple qualitative description of the action potential. The depolarizing “upswing” of the action potential is due to the opening of Na⁺ channels. Recall that Na⁺ has a positive equilibrium potential, so when Na⁺ channels open the voltage shifts towards the Na⁺ equilibrium potential. The repolarization back to a negative membrane potential is due to closure of those Na⁺ channels, with help from K⁺ channels that open somewhat more slowly than the Na⁺ channels. Recall K⁺ has a negative equilibrium potential, so opening of K⁺ channels will help with repolarization. Essential for action potential generation is the difference in equilibrium potentials of Na⁺ and K⁺, which causes the voltage to shift in opposite directions when Na⁺ vs K⁺ channels open.

For channels through which more than one ion type can permeate — e.g. non-selective cation channels — the reversal potential is the voltage at which there is no net current through the channel (0 mV for a non-selective cation channel). Opening of channels with a reversal potential more positive than the membrane potential will produce inward current and make the membrane potential more positive (as for Na⁺ channels); conversely opening channels with a reversal potential more negative than the membrane potential will produce outward current and make the membrane potential more negative (as for K⁺ channels). Another way to remember this is that inward movement of positive charge makes the inside of the cell and membrane potential more positive, and outward movement of positive charge makes the inside of the cell and membrane potential more negative.

These issues form the core of how action potentials are generated. Before reading the rest of the material below, make sure you are comfortable with the description above and the Membrane Potential chapter, which describes these properties of ions and membrane in more detail.

Resting potential

The resting potential refers to the voltage across the cell membrane in the absence of external stimuli (i.e. at “rest”). In other words, the resting potential is the difference between the voltage inside and outside the cell in the absence of external stimuli. The resting potential is dominated by open K⁺ channels, and hence is near the K⁺ equilibrium potential. Resting potential is not exactly equal to E_K because some other channels with different ion selectivity are also open when the cell is at rest. When multiple channels with different ion selectivities are open, the cell voltage reflects a weighted average of the associated reversal potentials. This is directly analogous to the concept of a reversal potential for a channel, now applied to an entire cell: the resting potential is the voltage at which there is no net current into or out of the cell, just as the reversal potential is the voltage at which there is no net current through a channel. This no net current situation is created when currents through all the open channels sum to 0. Since there is no net current into a cell at the resting potential, there is no net movement of charge into or out of the cell, and the voltage does not change. Typical resting potentials are near -70 mV.

Consider a simple example: a cell that contains only K⁺ and Na⁺ channels. If only K⁺ channels are open, the membrane potential will be equal to the K⁺ equilibrium potential, E_K. If only Na⁺ channels are open, the membrane potential will be equal to the Na⁺ equilibrium potential, E_Na. If an equal number of Na⁺ and K⁺ channels are open, and the conductance of each type of channel is the same, then the membrane voltage will be halfway between the K⁺ and Na⁺ equilibrium potentials – at this voltage current from K⁺ flowing out of the cell and Na⁺ flowing in will cancel such that there is no net current flow.

These same concepts determine both the resting potential and the change in voltage in response to a stimulus that alters the set of open channels – i.e. a stimulus can alter the membrane voltage by changing the relative number of open K⁺ and Na⁺ channels. In the example here, if we start with a cell with only K⁺ channels open and a stimulus opens Na⁺ channels such that an equal number of Na⁺ and K⁺ channels are open, the voltage will change from E_K to a voltage half way between E_K and E_Na. (This discussion neglects how quickly the voltage gets to the new value, so for now assume we are talking about a long-lasting stimulus and slow changes in voltage).

An important point here is that two distinct types of K⁺ channels contribute to the control of the action potential. “Leak” K⁺ channels, which do not show strong voltage dependence in their opening, are key determinants of the resting potential; as their name implies, these channels show a high level of constitutive activity (i.e. many are open when the cell is “at rest”). These are distinct from voltage-activated K⁺ channels that open during the action potential (see below) and close following return of the membrane potential to near its resting value.

We will now apply the concepts introduced above to understand how the key properties of action potentials listed earlier can be explained in terms of the underlying ion channels. Make sure you are comfortable with the material up to here before proceeding!

How is the action potential produced? An early idea due to Bernstein was that action potentials reflected a momentary breakdown in the membrane, such that for a brief moment the membrane became permeable to all ions. Such a breakdown in membrane permeability would permit all charged ions to cross the membrane, and thus create a current with a reversal potential of 0 mV. This current, in turn, would depolarize the cell from its normal resting potential towards (but not past) 0 mV. This hypothesis, however, is inconsistent with the observation that the peak voltage reached during the action potential can exceed 0 mV (e.g. Figure 1). For the membrane to reach positive potentials, the permeability to ions with positive equilibrium potentials (Na⁺ and/or Ca²⁺) must be higher than the permeability to ions with negative equilibrium potentials (K⁺ and Cl^–). Thus, action potentials must reflect a selective increase in permeability (via opening of channels) to ions with positive equilibrium potentials.

Our modern understanding of the action potential comes from beautiful work by Alan Hodgkin and Andrew Huxley. They used the squid giant axon — which is about the size of a cocktail straw — to control (rather than only measure) the membrane voltage and to replace permeable ions, such as Na⁺, with impermeable ions such as choline. This combination of voltage control and ion replacement allowed them to directly observe how voltage altered the flow of Na⁺ and K⁺ across the membrane. These experiments identified Na⁺ and K⁺ as the key ions responsible for the action potential and provided a detailed biophysical explanation for how action potentials are generated. The key role of Na⁺ explains why action potentials reach positive potentials: a sufficient number of Na⁺ channels open to drive the membrane potential close to the Na⁺ equilibrium potential.

How do we explain the abrupt threshold for action potential generation as in Figure 1? The opening of both the voltage-activated Na⁺ and K⁺ channels that dominate the action potential increases with depolarization. Na⁺ and K⁺ channels differ in two critical ways, however: the direction of current flow when the channels open, and the speed with which the channels open following a change in voltage.

The Hodgkin cycle

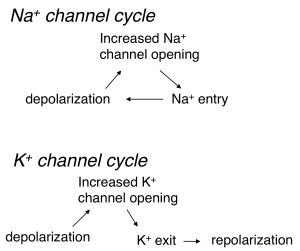
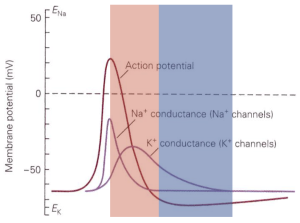
Depolarization and opening of K⁺ channels at voltages near action potential threshold leads to outward movement of K⁺ (since the voltage is depolarized relative to the K⁺ equilibrium potential). This outward K⁺ current repolarizes the cell — i.e. it counteracts the initial depolarization (Figure 3). This is a form of negative feedback because the effect of an external stimulus on voltage is opposed by K⁺ channel opening and the resulting current. The control of blood sugar by insulin release is another example of negative feedback: increased blood sugar leads to insulin release, which leads to movement of sugar from the blood into stores.

In contrast to the behavior of K⁺ channels, depolarization and opening of Na⁺ channels leads to an inward Na⁺ current, which leads to more depolarization (Figure 3). This is a form of positive feedback — which serves to amplify the initial depolarization. A microphone and connected speaker placed too close to each other provide a familiar example of positive feedback: the microphone detects sound from the speaker, amplifies it, plays it back through the speaker, detects it, amplifies it, … . We refer to this positive feedback behavior of Na⁺ channels as the Hodgkin cycle.

The threshold for action potential generation occurs when a depolarizing stimulus opens a sufficient number of Na⁺ channels such that the net current flowing into the cell is inward (i.e. the inward current through Na⁺ channels exceeds the outward current through K⁺ and Cl^– channels). At this critical voltage, the depolarization produced by the initial stimulus begins to be amplified through the positive feedback of the Hodgkin cycle. The inward current produced causes more Na⁺ channels to open, more inward current, more depolarization, … . Once the cell enters this positive feedback cycle, there is no turning back until all available Na⁺ channels have opened and the membrane potential approaches the Na⁺ equilibrium potential. This sequence of events is what underlies the discrete nature of the action potential.

Repolarization and channel inactivation

The description above is missing a key step — getting the voltage back down to its resting value so that the cell can respond to a subsequent stimulus and generate another action potential. Two mechanisms allow the voltage to recover:

Na⁺ channels transition from the open state to an inactivated state. In the inactivated state the channels are effectively out of commission: they no longer permit Na⁺ ions into the cell, and they cannot reopen when subject to depolarization (Figure 4). Recovery from the inactivated state to the closed state (a state from which they can reopen) occurs very slowly at depolarized voltages and much more rapidly at substantially negative voltages – e.g. those close to the resting potential. This is a safety mechanism that effectively insures that Na⁺ channels do not continue to permit inward depolarizing current after the peak of the action potential has been reached. Efficient recovery of Na⁺ channels to the closed state occurs only when the membrane has been repolarized to near the resting potential – and hence only then are channels available for opening.

K⁺ channels open more slowly than Na⁺ channels, and this slowed opening means that K⁺ channel opening occurs at an ideal time to help the voltage recover back to the resting potential.

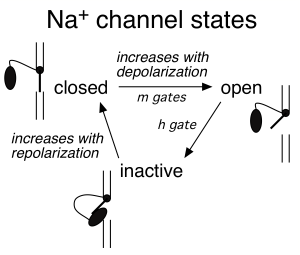
Figure 5 summarizes the time course of the opening of Na⁺ and K⁺ channels during the action potential.

One of the key contributions Hodgkin and Huxley made was to develop a simple model that captured the kinetics of channel opening and closing. This model relies on several “gates” that account for the transitions of Na⁺ and K⁺ channels between different states. The importance of this description was that it made clear predictions about the structure of ion channels – predictions that turned out to be quite accurate:

m: Na⁺ channel activation gate (see Figure 4)

• opens by depolarization
• resets to “ready” position rapidly by repolarization after the h gate is reset
• Aside: opening of several m gates is required for channel opening. We now know those gates represent different channel subunits

h: Na⁺ channel inactivation gate

• causes channel to cease to permit Na⁺ entry into the cell
• inactivation develops with time after activation gates open – i.e. activation of h gate is triggered by activation of m gates, not by voltage directly.
• h gate is reset by membrane repolarization
• Aside: we now know that the h gate is produced by a globular protein moiety attached to a flexible tether; this protein moiety can plug the channel pore (the “ball-and-chain” model; see elliptical black ball in Figure 4 schematics)

n: K channel activation gate

• activates in response to depolarization
• resets in response to repolarization

Alterations in the properties of these gates are important clinically. Amazingly, the empirical description Hodgkin and Huxley came up with to describe their data has proven to be an accurate description of how ion channels work at a molecular level (remember next to nothing was known about channels when they did their work).

The state of the cell’s ion channels immediately following an action potential is very different than it was prior to the action potential. Many Na⁺ channels are still in the inactive state, since recovery from inactivation occurs rapidly only at negative voltages and then takes some time (a few ms) to complete. And extra voltage-gated K⁺ channels are open, thus causing the membrane potential to be more tightly tied to the K⁺ equilibrium potential than normal. These two effects create the refractory period — a period following an action potential during which the cell is either completely unable (absolute refractory period, typically lasting a few ms) or resistant (relative refractory period, often lasting tens of ms) to generating another action potential (Figure 6). The absolute refractory period occurs when there are not enough Na⁺ channels available for opening to enter the positive feedback Hodgkin cycle; in this period, it is impossible for the cell to generate an action potential no matter how strongly it is stimulated. During the relative refractory period, enough Na⁺ channels have recovered from inactivation to produce an action potential, but a larger stimulus is required to reach action potential threshold because many Na⁺ channels still are in the inactivated state and some voltage-activated K⁺ channels remain open and hence make it harder for a stimulus to change the voltage and get to threshold.