Membrane Potentials

Standard laws of electricity govern how cells make electrical signals across their membranes. This chapter reviews these laws. The need to think about electricity may seem daunting to some biologists, but really it is not particularly compli­cated. Electricity obeys a few simple physical rules in a logical manner. You have studied them before. Comfort with the key concepts in this chapter will be very helpful in subsequent more specific and detailed study of electro­phys­iology. As we will see, if you have both (i) gradients of ions across a membrane and (ii) a membrane perme­ability to some of these ions by open ion channels, the necessary net flow of the charged ions in these channels forms an electric current and can change the membrane potential.

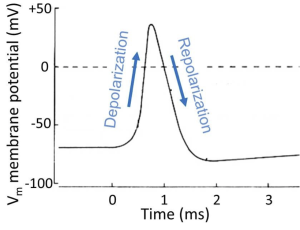
To motivate our study of principles, we look ahead at a nerve cell sending an electrical message, the spike-like action potential (we will examine this process in more detail later in the course). The action potential is a stereo­typed, efficient, brief, electrical signal that can travel regeneratively at high speed along an axon. It is the long-distance, electrical message of the nervous system, the unit of information like the information bits in the wires of a com­puter. Figure 1 is an electrical recording from the inside of an active nerve cell. We will note just three typical properties for now. (i) This neuron starts with a NEGATIVE inside resting potential (-60 mV). (ii) During the action potential, the inside of the cell becomes briefly POSITIVE. And (iii) the whole signal is finished in <1 ms (0.001 s). Think of this signal as a brief membrane potential excur­sion of about 100 mV, the pulse-like unit of propagated information. We will begin to explain in physi­cal terms how cells make electrical signals like this and how they propagate.

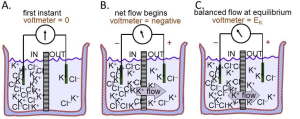
A thought experiment on membrane potentials

We now use these rules of elec­tricity to describe the origin of membrane potentials (Figure 2). Again electrolyte in a beaker is divided by a mem­brane containing only K⁺ channels. But now there is no pulse generator, just a recording ampli­fier that reports any potential difference that might appear spon­taneously across the membrane. These com­partments, for example, could represent the inside and the out­side of a cell with a K⁺-perme­able mem­brane since this time, more like a real cell, the IN com­part­ment con­tains high K⁺, and the OUT com­partment, low K⁺ (Figure 2A). Each solution is initially electrically neutral with an equal number of anions and cations, and the volt­meter cartoon indicates that there is initially no poten­tial difference between them. Rule 2 and your intuition say that K⁺ ions will start to flow towards the OUT compartment because they are free to diffuse down their concen­tra­tion gradient (Fig. 3B). Since there are no Cl^– chan­nels in the mem­brane, there is no move­ment of Cl^– ions across this mem­brane. Thus, there is a net move­ment only of positive charges, and Rule 3 says that the outward K⁺ flow carries an out­ward electric current I_K. Rule 4 says that since positive charge is being removed from the IN compart­ment, that com­partment starts to become more nega­tive–as indicated by the second voltmeter cartoon. A membrane potential has been generated!

However, rule 2 says that the net flow of K⁺ cations will soon slow down as they experi­ence an electrical retar­ding force from the grow­ing membrane poten­tial that makes it progressively harder for them to leave the negative IN com­part­ment. An equilibrium is reached as the opposing electrical force pulling K⁺ ions back becomes equal to the diffusion force pushing them out (Fig. 3C). The forces have become balanced. Now the membrane has established a stable negative internal membrane potential all by itself! This whole process takes only a millisecond or two. The potential difference arose because (i) there is a K⁺ gradient, and (ii) the membrane has K⁺-selective ion channels. This thought experi­ment corresponds very closely to the situation in real cells. They have K⁺ inside and they have a negative resting potential inside (Fig. 1) because of a pre­domi­nance of open K⁺ channels at rest. We have applied Rule 4 to understand the negative resting potential and now generalize with the most important concept to understand electrical signaling:

Our last rule of electricity says that very few ions need to move to produce sizable changes in membrane potential:

Capacitance:  Electrical capacitors store charge. Recall that a substance like the lipid bilayer that does not conduct electricity is called an insulator. Two conductors separated by a thin insu­lator form an electrical capacitor. Therefore, the thin plasma membrane bathed by inside and outside conducting electro­lyte solutions has the property of an electrical capa­citor. The magnitude of a capaci­tance (sym­bolized C) is defined as the number of charges that you have to put on the capacitor to achieve a certain potential change. There­fore, the capa­ci­tance of cell mem­branes tells us how many ions have to be moved across the membrane to change the membrane potential during signaling. For a spherical neuron 20 m in diameter, a net move­ment of only ~10^-17 moles of cations into the cell will be enough to make the inside 100 mV more positive–equi­valent to one action potential. This move­ment amounts to only 0.002% of the number of cations already in the cell (~6×10^-13 moles). Therefore, the ion fluxes needed to make signals in biological membranes are tiny, and the charge movement and potential changes can be completed quickly. However, after repeated bouts of sig­nal­ing it becomes essential to accelerate ion pumps to restore the gradually declining ion gradients. This need for accelerated pumping is accentuated in fine nerve processes where a large surface-to-volume ratio means that the reserve pool of ions inside is smaller.

The three questions approach

We begin with three questions that will allow us to determine what each ion can do to the membrane potential. We have just applied these questions to the K⁺ ion in Figure 3. Now we generalize. No equations, just simple logic that goes a long way.

Question 1: Which ion is permeable?

Question 2: Which direction does it want to flow?

Question 3: What membrane potential would that induce?

For Figure 2, the three answers were:

• K⁺ is permeable;
• It would flow OUT;
• That would make the voltage of the IN side negative.

Now you can go through each of the ions in Table 1, supposing that the membrane is selectively per­meable only to K⁺, Na⁺, Ca²⁺, or Cl^– one at a time, using the three questions to decide what sign of membrane potential would result. You should have found two ions that could make the mem­brane potential negative and two that could make it positive. Excitable cells open and close ion channels to each of these ions to generate their electrical signals. In particular, you will learn shortly that for the nerve cell in Figure 1, the resting membrane is K⁺ permeable and therefore negative inside; the membrane during the action potential becomes Na⁺ permeable (Na⁺ channels open) and therefore a few Na⁺ ions move in and the potential becomes positive; and then the Na⁺ channels close, and K⁺ channels bring the membrane back to the negative resting potential.

Recap

Let us apply our learning to the action potential (AP) rising phase in anticipation of your next session on electrical excitability. The AP rising phase requires net entry of Na⁺ ions (Rule 3). The number of ions moving is modest (Rule 6). Nevertheless, repe­titive firing of APs will lead to intracellular Na⁺ accumulation, so, since its Na⁺ substrate increases, the Na⁺/K⁺-ATPase pump speeds up and pumps the Na⁺ out again more vigorously. Local glucose metabolism speeds up a bit to make the needed ATP. A brain imaging technique called PET scan measures glucose consumption and allows radiologists to observe which brain regions become active during specific mental activities. Soon, you will also learn that our larger nerve fibers often use myelin as a way to reduce the electrical capacitance of sections of axon. In myelinated nerve, Schwann cell membranes are wrapped on top of each other in many tight layers around the axon, reducing the effective capacitance and reducing the amount of ion movement needed to make an action potential. This permits faster depolarizations with smaller Na⁺ flow (Rule 6) and faster propagation of the action potential message. We will return to this later.

The Nernst Equation

So far we have been thinking qualitatively about the sign of the mem­brane potential, and that suffices for basic understanding. However, sometimes we want to say how large the membrane potential will be rather than just working out its sign. Scientists need to do this to check that they really understand what is going on. For this, we return to the thought experiment of Figure 2. In the right panel, the membrane potential comes to an equilibrium value where the concen­tration force pushing K⁺ ions out of the IN compartment is exactly matched by the electrical force pulling them back. This is an electrochemical equilibrium and therefore ther­mo­dynamics can give us an expression for the equilibrium potential. Since the problem involves a membrane selectively permeable only to K⁺ ions, we call this the “potassium equi­li­brium potential” symbolized by E_K. For completeness we write the answer called the Nernst Equation first in its general thermo­dyna­mic form for any ion with charge z, but then follow by writing a much more practical version for our body temperature in millivolts. If you do need to calculate equilibrium potentials, use the practical form. You should under­stand the signifi­cance of the Nernst Equa­tion as a beautiful and compact explanation, but in general prac­tice, you would rarely have to use it.

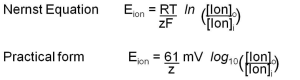
In the formal first form, there are thermodynamic constants: R (gas constant), T (temperature), and F (Faraday’s number). In the practical form, their values have already been factored in for 37ºC. Notice that the equili­brium potential depends on the ratio of the ion concentration outside and inside. The ratio appears inside a loga­rithm. Box C reminds us that log₁₀ (x) equals the power of 10 that would give the value x. It is also a button on your calculator!

Conceptual Significance of the Nernst Equation

With the practical form of the Nernst equation, we can plug in the ion concentrations listed in the chapter on Cell Membranes and Transporters to get the equilibrium potentials of each of the four important ions (Table 1). These values define the range of plasma membrane potentials that cells are able to achieve. As expected from the three-questions approach, E_K is a nega­tive number, -97 mV. That is as far negative as the plasma membrane potential ever gets. To do so, the membrane would have to be exclusively permeable to K⁺ ions; that is, the only ion channels open would be K⁺ channels. In resting axons, open K⁺ channels greatly outnumber open Na⁺, Cl^–, and Ca²⁺ channels so the plasma membrane is primarily permeable to K⁺, and the resting potential approaches E_K. By contrast, but as expected from the three-question approach, E_Na is a posi­tive number, +65 mV. As you will see shortly, E_Na sets the positive limit of the nerve action potential (Figure 1) when mostly Na⁺ channels are open. Remember that at the equilibrium potential for an ion, the diffusion force and the electrical force are exactly balanced (they cancel each other) and there would be no further net flow of that ion. In several disease or nutritional conditions the ion gradients across our cell membranes change. This can severely impact the resting potential and the electrical signaling of nerve and muscle.

Key concept

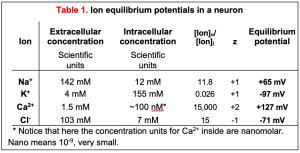
Real membranes have several types of open channels. Although we say the resting potential is nega­tive because K⁺ channels are open there, the resting potential is never as negative as the ideal E_K (-97 mV). This is because even at rest, there are some open Na⁺ and Cl^– channels whose equilibrium potentials are more positive than E_K (+65 and -71 mV in Table 1 for neurons). When several different channels are open simultaneously, the membrane potential (V_m) will lie somewhere between the equilibrium potentials of each of those channels. Thus, if the conductance to K⁺ is the largest at rest, V_m will be brought closer to E_K, and if the conductance to Na⁺ rises, V_m will depolarize, eventually approach­ing E_Na if the Na⁺ conductance becomes the largest. This important concept will explain how excitable cells make electrical signals (membrane potential changes) in the nervous system by opening and closing ion-selective channels.